When the current in a toroidal solenoid is changing at a rate of 0.0260 A/s, the magnitude of the induced emf is 12.6 mV. When the current equals 1.40 A, the average flux through each turn of the solenoid is 0.00285 Wb. How many turns does the solenoid have?

Verified step by step guidance

1. Identify the given values: rate of change of current (\( \frac{dI}{dt} \)) is 0.0260 A/s, induced emf (\( \mathcal{E} \)) is 12.6 mV or 0.0126 V, current (I) is 1.40 A, and average flux per turn (\( \Phi \)) is 0.00285 Wb.
2. Use Faraday's Law of Electromagnetic Induction which states \( \mathcal{E} = N \frac{d\Phi}{dt} \), where N is the number of turns in the solenoid and \( \frac{d\Phi}{dt} \) is the rate of change of magnetic flux.
3. Calculate the total change in flux (\( \frac{d\Phi}{dt} \)) using the relationship between flux and current. Since \( \Phi = N \cdot \phi \) where \( \phi \) is the flux per turn, and the current is changing, use \( \frac{d\Phi}{dt} = N \cdot \frac{d\phi}{dt} \).
4. Substitute the expression for \( \frac{d\Phi}{dt} \) in terms of \( \frac{dI}{dt} \) and \( \phi \) into Faraday's Law equation. Solve for N by rearranging the equation to isolate N on one side.
5. Plug in the values for \( \mathcal{E} \), \( \frac{dI}{dt} \), and \( \phi \) to calculate the number of turns, N.

Key Concepts

Faraday's Law of Electromagnetic Induction

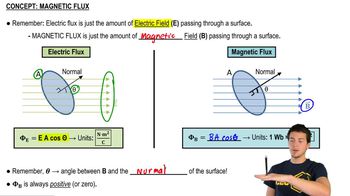
Faraday's Law states that a change in magnetic flux through a circuit induces an electromotive force (emf) in the circuit. The induced emf is proportional to the rate of change of the magnetic flux. In this problem, the changing current in the solenoid leads to a changing magnetic field, which induces an emf according to this principle.

Magnetic Flux

Magnetic flux is a measure of the quantity of magnetism, taking into account the strength and the extent of a magnetic field. It is calculated as the product of the magnetic field and the area through which the field lines pass, perpendicular to the field. In this context, the average flux through each turn of the solenoid is given, which is crucial for determining the number of turns.

Inductance and Solenoids

Inductance is a property of an electrical conductor by which a change in current through it induces an emf in the conductor itself and in nearby conductors. A solenoid, a coil of wire, has inductance that depends on its number of turns, the area of the loops, and the core material. Understanding how these factors relate helps in calculating the number of turns in the solenoid.