Diffraction occurs for all types of waves, including sound waves. High-frequency sound from a distant source with wavelength 9.00 cm passes through a slit 12.0 cm wide. A microphone is placed 8.00 m directly in front of the center of the slit, corresponding to point O in Fig. 36.5a . The microphone is then moved in a direction perpendicular to the line from the center of the slit to point O. At what distances from O will the intensity detected by the microphone be zero?

Verified step by step guidance

1. Step 1: Understand the problem. This is a single-slit diffraction problem involving sound waves. The condition for destructive interference (intensity detected to be zero) is given by the equation: \( a \sin \theta = m \lambda \), where \( a \) is the slit width, \( \lambda \) is the wavelength of the sound wave, \( m \) is the order of the minimum (\( m = \pm 1, \pm 2, \pm 3, \dots \)), and \( \theta \) is the angle from the central axis to the point of zero intensity.
2. Step 2: Relate the angle \( \theta \) to the position \( y \) of the microphone. The geometry of the setup gives \( \tan \theta = \frac{y}{L} \), where \( L \) is the distance from the slit to the microphone (8.00 m in this case). For small angles, \( \sin \theta \approx \tan \theta \approx \frac{y}{L} \). Substituting this into the diffraction condition, we get \( a \frac{y}{L} = m \lambda \).
3. Step 3: Solve for \( y \), the distance from point O where the intensity is zero. Rearrange the equation to isolate \( y \): \( y = \frac{m \lambda L}{a} \). Here, \( m \) is the order of the minimum (\( m = \pm 1, \pm 2, \pm 3, \dots \)), \( \lambda = 9.00 \ \text{cm} = 0.0900 \ \text{m} \), \( L = 8.00 \ \text{m} \), and \( a = 12.0 \ \text{cm} = 0.120 \ \text{m} \).
4. Step 4: Substitute the known values into the equation. For each order \( m \), calculate \( y \) using \( y = \frac{m \lambda L}{a} \). For example, for \( m = 1 \), \( y = \frac{(1)(0.0900)(8.00)}{0.120} \). Repeat this for \( m = 2, 3, \dots \) until the values of \( y \) exceed the physical limits of the setup.
5. Step 5: Interpret the results. The calculated \( y \) values represent the distances from point O where the intensity detected by the microphone will be zero. These positions correspond to the locations of destructive interference caused by the diffraction of the sound wave through the slit.

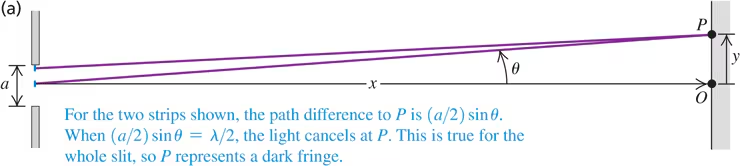
Key Concepts

Diffraction

Diffraction is the bending of waves around obstacles and the spreading of waves when they pass through narrow openings. This phenomenon occurs for all types of waves, including sound, light, and water waves. The extent of diffraction depends on the wavelength of the wave relative to the size of the opening or obstacle. In this scenario, the sound waves from the source will diffract as they pass through the slit, leading to variations in intensity at different points.

Interference

Interference is the phenomenon that occurs when two or more waves overlap and combine to form a new wave pattern. This can result in constructive interference, where wave amplitudes add together, or destructive interference, where they cancel each other out. In the context of the microphone's position, points of zero intensity correspond to locations where destructive interference occurs due to the path difference between waves arriving from different parts of the slit.

Path Difference

Path difference refers to the difference in distance traveled by two waves arriving at a point from different sources or parts of a wavefront. For destructive interference to occur, the path difference must be an odd multiple of half the wavelength. In this problem, calculating the path difference for sound waves reaching the microphone from various points along the slit will help determine the specific distances from point O where the intensity is zero.