
Improve Math Test Scores by Asking the Right Questions

Every college math instructor has been there. The students have been actively engaged in class. They’ve completed their homework (for the most part). The majority have even turned in the test review that you provided. Yay! Then you grade the tests. Questions were left blank, many scored shockingly low, and several students left sad notes in the margins. Some did well, but so many failed that the bell curve is upside-down! How is it they learned so little?!
Then, we dive into the ice cream to ease the pain (or maybe that’s just me).
Well, put the ice cream back in the freezer, my friends, because there is hope! A few tweaks to the way you design test exercises could potentially improve test scores and right that bell curve, not by lowering standards, but by more accurately assessing student knowledge by asking more focused test questions.
How many levels of cognition are you assessing?
One of the challenges that college math students face is that most math exercises require several levels of cognition and a variety of mastered objectives. Consider the exercise: “Solve 5𝑥(𝑥−2) = 3𝑥−2.”
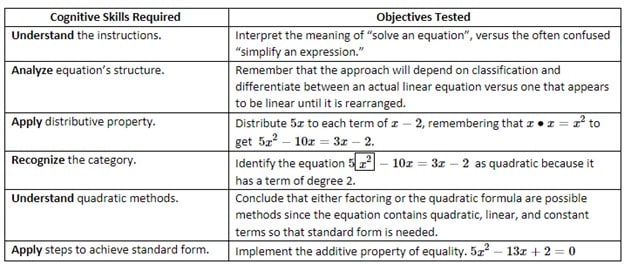
The student must remember, understand, apply, and analyze just to get the equation in a form in which quadratic methods can be applied. This single test question contains the first four of the six levels of cognition described in Bloom’s Taxonomy. This might seem great, but if the student falters on any one of them, the subsequent skills may not be demonstrable, which is not so great. So, consider including items that test intermediate steps and fewer cognitive skills. The questions can be multiple choice, or other formats. Be creative! Here are some examples.
- Explain why 5𝑥(𝑥−2)=3𝑥−2 is not a linear equation.
- What is the standard form of the equation 5𝑥2−10𝑥=3𝑥−2?
- Which quadratic method would you choose for solving 5𝑥2−13𝑥+2=0 and why?
- A student decided to solve 5𝑥2−10𝑥=3𝑥−2 using the quadratic formula. Which values should the student use for 𝑎, 𝑏, and 𝑐? How do you know?
- Name all four quadratic methods we discussed in class.
- Give an example of a quadratic equation in standard form.
- Consider the instructions “Solve 5𝑥(𝑥−2)=3𝑥−2,” versus “Simplify 5𝑥(𝑥−2)=3𝑥−2." Which instructions are correct, and why?
- What is the first step in solving the equation 5𝑥2−10𝑥=3𝑥−2?
You get the idea! Since I began incorporating questions like these, as well as knowledge level questions about vocabulary and notation (more on that in my next post), I find my test scores tend to fit a more normal distribution. There are other benefits, too. The students are encouraged when they receive credit for the knowledge they do have and they can more readily identify the specific skills they lack. If you find anything in this post helpful, or if you have tried similar approaches, I would love to hear about it! Thank you for reading!
About the author

Quin Hearn, M.S., Broward College
Quin Hearn was born in Vandenburg Air Force Base, California where her father worked at the Western Space and Missile Center. Her father’s work on the Space Shuttle program ultimately brought Quin to Florida where she attended the University of South Florida. Upon completion of her baccalaureate degree in mathematics, she accepted a Teaching Assistantship in the Department of Mathematics at Louisiana State University in Baton Rouge where she received her master’s degree. Since her return to Florida in 1998, Quin has held tenured faculty and department chairperson positions at Eastern Florida State College, Miami Dade College, and Broward College. In addition to teaching at Florida colleges, Quin created a popular YouTube channel with mathematics tutorial videos, www.youtube.com/mshearnmathematics and writes a variety of educational materials in the field of mathematics.



