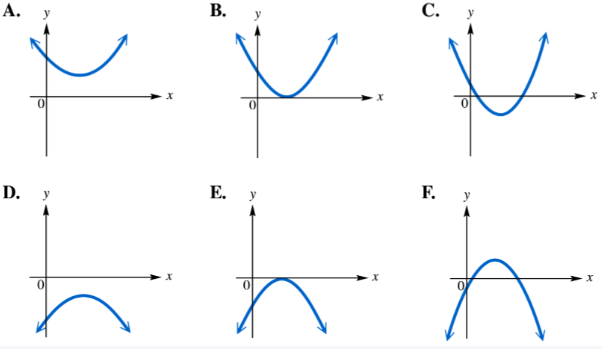
Several graphs of the quadratic function ƒ(x) = ax² + bx + c are shown below. For the given restrictions on a, b, and c, select the corresponding graph from choices A–F. (Hint: Use the discriminant.) a < 0; b² - 4ac = 0

Verified step by step guidance

1. Recall the quadratic function is given by \(f(x) = ax^2 + bx + c\), where \(a\), \(b\), and \(c\) are constants.
2. Note the given conditions: \(a < 0\) and the discriminant \(b^2 - 4ac = 0\). The discriminant tells us about the nature of the roots of the quadratic.
3. Since \(b^2 - 4ac = 0\), the quadratic has exactly one real root, meaning the graph touches the x-axis at exactly one point (a repeated root).
4. Because \(a < 0\), the parabola opens downward, so the vertex is a maximum point and the graph is concave down.
5. To select the correct graph, look for the parabola that opens downward and just touches the x-axis at one point (the vertex), reflecting the repeated root condition.

Key Concepts

Quadratic Function and Its Graph

A quadratic function is a polynomial of degree two, expressed as ƒ(x) = ax² + bx + c. Its graph is a parabola that opens upward if a > 0 and downward if a < 0. The coefficients a, b, and c determine the shape and position of the parabola on the coordinate plane.

Discriminant of a Quadratic Equation

The discriminant, given by b² - 4ac, indicates the nature of the roots of a quadratic equation. If the discriminant equals zero, the quadratic has exactly one real root (a repeated root), meaning the parabola touches the x-axis at a single point (vertex).

Effect of Coefficient 'a' on Parabola Orientation

The sign of the coefficient 'a' determines the direction the parabola opens. If a < 0, the parabola opens downward, forming a maximum point at the vertex. This affects the graph's shape and helps identify the correct graph when combined with other conditions.