A speed skater accelerates from rest and then keeps skating at a constant speed. Draw a complete motion diagram of the skater.

Draw a pictorial representation for the following problem. Do not solve the problem. What acceleration does a rocket need to reach a speed of 200 m/s at a height of 1.0 km?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
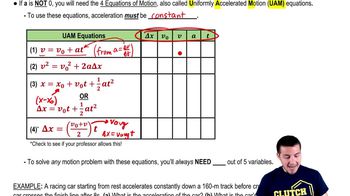
Key Concepts
Acceleration

Kinematics
Height and Gravity

A bowling ball rolls up an incline and then onto a smooth, level surface. Draw a complete motion diagram of the bowling ball. Don't try to find the acceleration vector at the point where the motion changes direction; that's an issue for Chapter 4.
Your roommate drops a tennis ball from a third-story balcony. It hits the sidewalk and bounces as high as the second story. Draw a complete motion diagram of the tennis ball from the time it is released until it reaches the maximum height on its bounce. Be sure to determine and show the acceleration at the lowest point.
How many significant figures are there in each of the following values?
75.0
How many significant figures are there in each of the following values?
0.07 x 108
Convert the following to basic SI units or a combination of basic SI units:
62 ft/day
