You are watching a jet ski race. A racer speeds up from rest to 70 mph in 10 s, then continues at a constant speed. Draw a basic motion diagram of the jet ski, using s from the video, from its start until 10 s after reaching top speed.

FIGURE EX1.9 shows five points of a motion diagram. Use Tactics Box 1.2 to find the average acceleration vectors at points 1, 2, and 3. Draw the completed motion diagram showing velocity vectors and acceleration vectors.

 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Average Acceleration
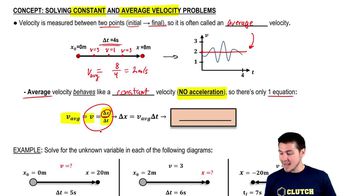
Motion Diagrams

Vector Representation

You drop a soccer ball from your third-story balcony. Use the particle model to draw a motion diagram showing the ball's position and average velocity vectors from the time you release the ball until the instant it touches the ground.
FIGURE EX1.8 shows the first three points of a motion diagram. Is the object's average speed between points 1 and 2 greater than, less than, or equal to its average speed between points 0 and 1? Explain how you can tell.
FIGURE EX1.10 shows two dots of a motion diagram and vector. Copy this figure, then add dot 4 and the next velocity vector if the acceleration vector at dot 3 points left.
A speed skater accelerates from rest and then keeps skating at a constant speed. Draw a complete motion diagram of the skater.
A bowling ball rolls up an incline and then onto a smooth, level surface. Draw a complete motion diagram of the bowling ball. Don't try to find the acceleration vector at the point where the motion changes direction; that's an issue for Chapter 4.
