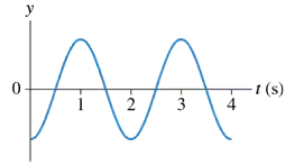
A block is suspended from a spring, pulled down, and released. The block's position-versus-time graph is shown in FIGURE P2.38. b. Draw a reasonable velocity-versus-time graph.

Video transcript

Hey, everyone in this problem, a block of mass M is attached to a spring and is set to oscillate with equal displacement. On either side of the equilibrium position, we're asked to determine how the block's velocity time graph would be. Its position. Time graph is shown in the figure. So we're given this figure of the position time graph. So on the vertical or Y axis, we have the position X at time T and along the horizontal or X axis, we have the time in seconds. Now this position starts at the maximum. OK. It decreases to the minimum And then increases again in completing two full oscillations. We're given four answer choices. They are all figures as well and they are figures of the velocity versus time. OK. So the velocity is on the vertical axis and the time in seconds is on the horizontal axis. Option A, the velocity starts at zero and decreases day before increasing up to the maximum And completing two full oscillations. Option B, the velocity starts almost at its maximum, Decreases to its minimum before increasing back up to its maximum. Complive two full oscillations. Option C the velocity starts at its minimum Increases up to its maximum before coming back down to its minimum and completing two full oscillations. and option D The velocity starts at zero and increases up to its maximum before decreasing Down to its minimum and again completing two full oscillations. So the problem is asking us, what will the velocity time graph look like? And we're given this position time graph. Now we have to remember how the velocity time graph and position time graph are related. OK. Well, recall the velocity V is equal to the derivative of the position D X divided by D T. What this means is that the velocity is equal to the slope of the position time curve. So we're given this position time curve and we're looking for the velocity time curve. Now we can pick out points that are easy to deal with. First, we know that the velocity is the slope of the X T curve. So let's look where we have particular slopes every time the position changes direction we get a slope of zero. OK. So at the very maximum and very minimum points, we have a slope of zero. If we have a slope of zero, that means that our velocity is equal to zero at this point. OK. So we have our velocity equals zero at the points where the position changes direction. OK. So if we compare this to the answer choices we were given That should mean that we have zero velocity corresponding with each of these markers on the horizontal axis. OK. So I'm drawing where The slope should be zero. OK? Where the velocity should be zero based on our position curve. And from just that information, we can already eliminate two of the answer choices. OK? For option B and option C, these zero velocities don't match. OK. The points where we should have zero velocity because we have zero slope in our position. Time graph do not match with where we have zero velocity in these curves. OK? So we're looking at answer choice, either A or D. Now the difference between A and D A starts at zero the velocity and decreases whereas D starts at zero and increases. Let's look at our position time curve at zero and the position is at its maximum, then the position decreases. We have a negative slope. If we have a negative slope, that means we have a negative velocity. So we have a negative velocity along the first part of our curve which means that we should start from zero and go downwards in our velocity curve. Yeah, we should be going downwards in our velocity curve, not upwards. So we can also eliminate option D and we therefore have option A is the correct answer. This looks like the velocity time curve that would match given the position time curve. And the correct answer is option A. Thanks everyone for watching. I hope this video helped see you in the next one.