How far has the car traveled when it reaches 60 mph? Give your answer both in SI units and in feet.

A speed skater moving to the left across frictionless ice at 8.0 m/s hits a 5.0-m-wide patch of rough ice. She slows steadily, then continues on at 6.0 m/s. What is her acceleration on the rough ice?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
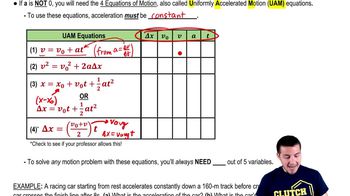
Key Concepts
Acceleration

Kinematics
Friction

A jet plane is cruising at 300 m/s when suddenly the pilot turns the engines up to full throttle. After traveling 4.0 km, the jet is moving with a speed of 400 m/s. What is the magnitude of the jet's acceleration, assuming it to be a constant acceleration?
When you sneeze, the air in your lungs accelerates from rest to 150 km/h in approximately 0.50 s. What is the magnitude of the acceleration of the air in m/s2?
A Porsche challenges a Honda to a 400 m race. Because the Porsche's acceleration of 3.5 m/s2 is larger than the Honda's 3.0 m/s2, the Honda gets a 1.0 s head start. Who wins? By how many seconds?
FIGURE EX1.18 shows the motion diagram of a drag racer. The camera took one frame every 2 s. Make a position-versus-time graph for the drag racer. Because you have data only at certain instants, your graph should consist of dots that are not connected together.
Write a short description of the motion of a real object for which FIGURE EX1.20 would be a realistic position-versus-time graph.
