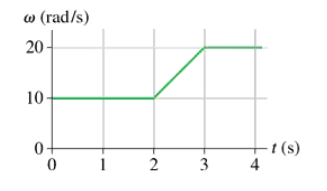
FIGURE EX4.23 shows the angular-velocity-versus-time graph for a particle moving in a circle. How many revolutions does the object make during the first 4 s?

Verified step by step guidance

1. Step 1: Understand the problem. The graph provided shows angular velocity (ω) in radians per second versus time (t) in seconds. To find the number of revolutions during the first 4 seconds, we need to calculate the angular displacement (θ) in radians and then convert it to revolutions. Recall that 1 revolution corresponds to 2π radians.
2. Step 2: Break the graph into segments for the first 4 seconds. From t = 0 to t = 2 seconds, ω increases linearly from 0 to 10 rad/s. From t = 2 to t = 4 seconds, ω remains constant at 10 rad/s.
3. Step 3: Calculate the angular displacement for the first segment (t = 0 to t = 2 seconds). Use the formula for angular displacement: θ = ∫ω dt. Since ω increases linearly, the area under the graph forms a triangle. The area of the triangle is (1/2) × base × height, where base = 2 s and height = 10 rad/s.
4. Step 4: Calculate the angular displacement for the second segment (t = 2 to t = 4 seconds). Since ω is constant at 10 rad/s, the area under the graph forms a rectangle. The area of the rectangle is base × height, where base = 2 s and height = 10 rad/s.
5. Step 5: Add the angular displacements from both segments to find the total angular displacement in radians. Convert this value to revolutions by dividing by 2π. This will give the total number of revolutions during the first 4 seconds.

Key Concepts

Angular Velocity

Angular velocity is a measure of how quickly an object rotates around a central point, expressed in radians per second (rad/s). It indicates the rate of change of the angular position of the object. In the context of circular motion, it is crucial for understanding how fast the object is moving along its circular path.

Area Under the Curve

In a graph of angular velocity versus time, the area under the curve represents the angular displacement of the object. This is because angular displacement can be calculated by integrating angular velocity over time. For a constant angular velocity, this area can be calculated as a rectangle, while for varying angular velocities, it may involve calculating the area of trapezoids or other shapes.

Revolutions

A revolution refers to one complete turn around a circular path. It is a unit of angular displacement, where one revolution corresponds to an angular displacement of 2π radians. To find the number of revolutions made by an object, the total angular displacement (in radians) can be divided by 2π.