Two blocks with masses mA and mB are connected by a massless string over a massless, frictionless pulley. Block B, which is more massive than block A, is released from height h and falls. A 1.0 kg block and a 2.0 kg block are connected by a massless string over a massless, frictionless pulley. The impact speed of the heavier block, after falling, is 1.8 m/s. From how high did it fall?

The spring shown in FIGURE P10.54 is compressed 50 cm and used to launch a 100 kg physics student. The track is frictionless until it starts up the incline. The student's coefficient of kinetic friction on the 30° incline is 0.15. What is the student's speed just after losing contact with the spring?
<Image>
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Hooke's Law

Conservation of Energy

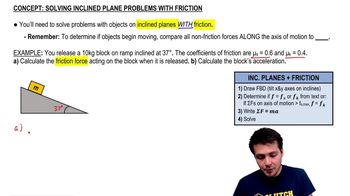
Friction and Inclined Planes
A freight company uses a compressed spring to shoot 2.0 kg packages up a 1.0-m-high frictionless ramp into a truck, as FIGURE P10.52 shows. The spring constant is 500 N/m and the spring is compressed 30 cm. What is the speed of the package when it reaches the truck?
The ice cube is replaced by a 50 g plastic cube whose coefficient of kinetic friction is 0.20. How far will the plastic cube travel up the slope? Use work and energy.
FIGURE 10.23 showed the potential-energy curve for the O2 molecule. Consider a molecule with the energy E1 shown in the figure. a. What is the maximum speed of an oxygen atom as it oscillates back and forth? Don't forget that the kinetic energy is the total kinetic energy of the system. The mass of an oxygen atom is 16 u, where 1u=1 atomic mass unit =1.66×10−27 kg .
A sled starts from rest at the top of the frictionless, hemispherical, snow-covered hill shown in FIGURE P10.56. a. Find an expression for the sled's speed when it is at angle ϕ .
CALC A 2.6 kg block is attached to a horizontal rope that exerts a variable force Fx = (20 − 5x) N, where x is in m. The coefficient of kinetic friction between the block and the floor is 0.25. Initially the block is at rest at x = 0 m. What is the block's speed when it has been pulled to x = 4.0 m?
