On level ground a shell is fired with an initial velocity of 40.0 m/s at 60.0° above the horizontal and feels no appreciable air resistance. Find its maximum height above the ground.

Question

Accepted Answer

Hey everyone. So today we're dealing with the problem about projectile motion and uniformly accelerated motion. So the problem states that we have a seat that can be launched at a velocity as high as 70 m per second. And in one specific instance it is observed to be launched at 70 m per second at an angle to the ground of 22.3 degrees above the horizontal. With this information neglecting air resistance, we are being asked to find the maximum height that the projectile reaches above the ground. So before doing anything else, let us just conceptualize this visually. So assuming we have a projectile, this is our projectiles course of motion. A if it's being lodged at an angle an angle sata to the horizontal, then this means that since it's being launched at an angle the projectile, it has two components to it, since it's not just moving in unilaterally in one direction, it is moving both forward horizontally towards towards this way, but it also has a vertical component. So let's write that out. We have a horizontal component, R. X. And a vertical component, or why? Now the question again is asking us to find the maximum height reached above the ground. So height is therefore a vertical component of the motion. So we're going to be focusing primarily on the vertical component of the motion occurring here with that in mind, let's go ahead and no doubt what we know and what we don't know. So since we're dealing with uniformly accelerated motion, we need to use a couple variables that will always be standards. So we need to start off with our initial velocity, our acceleration, the time taken to travel the distance that we're looking for the final velocity and the change in height. Because we are again dealing with vertical motion. So that is essentially our displacement in a sense, or changing wise or not changing height just yet. But going through this again, since we're dealing with the vertical motion, this is the initial velocity in the Y direction, which is simply the initial velocity multiplied by sine of data. And this is because if we look at this as a right triangle, if we look at our diagram as a right triangle, then if we have an angle here and this is the hypotenuse and the vertical is opposite to the angle. Therefore we can use our trig identities. And we have so gotta tour if it is opposite to the hypotenuse then we go with sign. So it is signed data. Is the vertical aspect simplifying this, we get 70 m per second, multiplied by sine of 22.3 degrees 22. degrees. Given a final answer of 26.6 m/s. So that is our initial velocity in the Y direction. Our acceleration is pretty easy. It is just the negative force of gravity because we are acting against gravity. So that will simply be negative 9.8 meters per second square. We don't know our time and we're not given our time. So let's leave it at that. Our final velocity. Well, we're asking when it is at maximum height. So remember projectile motion. Even though I've drawn it as a triangle here follows more of a parabolic arc, which means at the highest point the vertical velocity will actually be zero because that is when it stops moving up and it starts coming back down. So at the highest point all motion will halt in the vertical direction. It will still be moving horizontally, but the vertical velocity will therefore be zero. Let's write that down, vertical velocity. The final velocity at maximum height will be 0m/s. And finally the change in height, the change in Y is what we are looking for. So we know three of the variables, the initial velocity, the acceleration, and the final velocity. So we can go ahead and start using one of the uniformly accelerated motion equations. So we can use the equation uh final velocity squared is equal to the initial velocity squared Plus two A times the displacement. Delta Y. We already know most of these values. So let's go ahead and plug them in. So we have zero squared and I'm leaving out the excuse me, I'm leaving out the variables just for the sake of simplicity multiplied. So initial velocity squared Plus two times negative 9.8. And finally we have delta Y. So simplifying this, we get that 19.6 Delta Y is equal to 26.6 Squared, so therefore Delta Y is equal to 26.6 Squared divided by and I'm going yeah, divided by 19.6, which will give us a final answer of 36.1 m. Therefore the maximum height achieved by the projectile at a velocity of 70 m per second and at an angle of 22. degrees above the horizontal will be answer choice C 36.1 m. I hope this helps. And I look forward to seeing you.

On level ground a shell is fired with an initial velocity of 40.0 m/s at 60.0° above the horizontal and feels no appreciable air resistance. Find its maximum height above the ground.

Verified video answer for a similar problem:

Key Concepts

Projectile Motion

Kinematic Equations

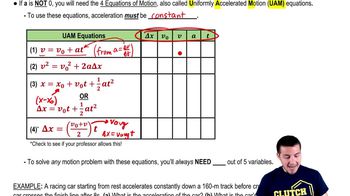
Trigonometric Decomposition