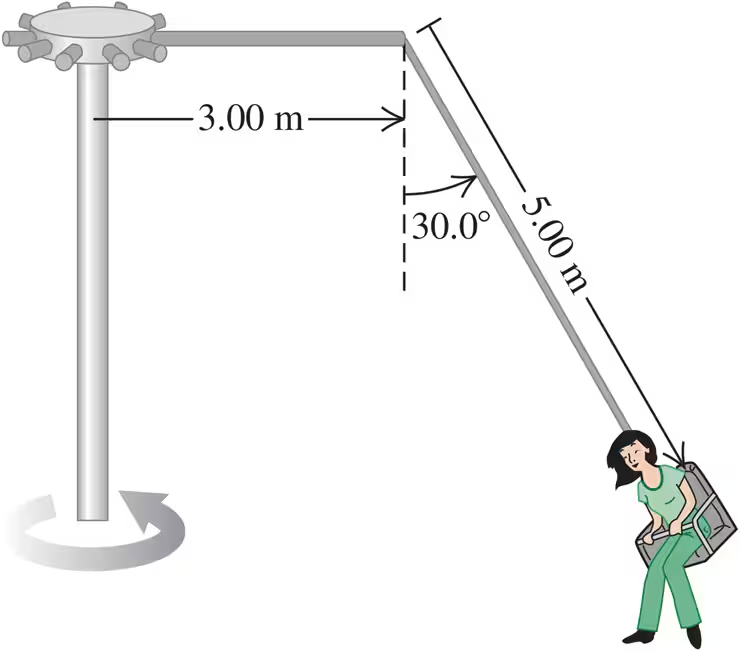
The 'Giant Swing' at a county fair consists of a vertical central shaft with a number of horizontal arms attached at its upper end. Each arm supports a seat suspended from a cable $5.00$ m long, and the upper end of the cable is fastened to the arm at a point $3.00$ m from the central shaft (Fig. E$5.50$). Find the time of one revolution of the swing if the cable supporting a seat makes an angle of $30.0°$ with the vertical.

Verified step by step guidance

1. Step 1: Analyze the geometry of the swing system. The cable length is given as 5.00 m, and it makes an angle of 30.0° with the vertical. Use trigonometry to determine the horizontal and vertical components of the cable's length. The horizontal component is given by \( L_{horizontal} = L \cdot \sin(\theta) \), and the vertical component is \( L_{vertical} = L \cdot \cos(\theta) \).
2. Step 2: Determine the radius of the circular motion. The radius is the sum of the horizontal distance from the central shaft to the cable attachment point (3.00 m) and the horizontal component of the cable's length calculated in Step 1. Use \( R = 3.00 \text{ m} + L_{horizontal} \).
3. Step 3: Apply the centripetal force equation to relate the tension in the cable to the circular motion. The centripetal force is provided by the horizontal component of the tension in the cable. Use \( F_{centripetal} = \frac{m \cdot v^2}{R} \), where \( v \) is the tangential velocity, \( R \) is the radius, and \( m \) is the mass of the seat and rider.
4. Step 4: Relate the forces acting on the cable. The vertical component of the tension balances the gravitational force, \( T_{vertical} = m \cdot g \). The horizontal component of the tension provides the centripetal force, \( T_{horizontal} = \frac{m \cdot v^2}{R} \). Use trigonometry to express \( T_{vertical} \) and \( T_{horizontal} \) in terms of the total tension \( T \) and the angle \( \theta \).
5. Step 5: Calculate the period of the swing's revolution. The tangential velocity \( v \) is related to the period \( T \) by \( v = \frac{2 \pi R}{T} \). Rearrange this equation to solve for \( T \), the time for one revolution: \( T = \frac{2 \pi R}{v} \). Substitute the values for \( R \) and \( v \) obtained from the previous steps.

Key Concepts

Centripetal Force

Centripetal force is the net force that acts on an object moving in a circular path, directed towards the center of the circle. In the context of the Giant Swing, this force is necessary to keep the seats moving in a circular motion as they swing outwards. It is provided by the tension in the cable and the gravitational force acting on the riders.

Pendulum Motion

Pendulum motion refers to the oscillatory movement of a mass attached to a fixed point by a cable or rod. In this scenario, the seats of the Giant Swing can be modeled as pendulums, where the angle of the cable with the vertical affects the period of the swing. The period is influenced by the length of the cable and the angle, which determines the effective gravitational force acting on the pendulum.

Period of Revolution

The period of revolution is the time it takes for an object to complete one full cycle of motion around a circular path. For the Giant Swing, this period can be calculated using the geometry of the swing and the forces acting on it. The angle of the cable and the length of the cable are critical in determining how quickly the swing completes its circular motion.