A cylindrical tungsten filament $15.0$ cm long with a diameter of $1.00$ mm is to be used in a machine for which the temperature will range from room temperature ( $20$ °C) up to $120$ °C. It will carry a current of $12.5$ A at all temperatures. What will be the maximum potential drop over the full length of the filament?

Question

Accepted Answer

Everyone. In this particular practice problem, we are asked to determine the greatest potential difference recorded over the entire length of the wire where we will have one m long night chrome wire with a circular cross section of a diameter 0.8 millimeter. Used for this experiment, There will be a constant current which will equal to 0.82 amp flowing through the wire at temperatures between 18 and 75°C. So first, I'm gonna start us off with pretty much creating a list of everything that we know here. So in this case, we will first have the length of the night chrome wire. So that will be the L. So the L is going to be one m long. And then from there, we'll have a diameter of 0.8 millimeter, 0.8 millimeter. But essentially, we wanted to be in the form of the radius. So that 0.4 millimeter or 0.4 times 10 to the power of minus three m. And then there will be a current flowing which will be at 0.82 M And the flow through the wire at temperature between 18 and 75°C. However, we have the data for the resistance city of Ni Chrome at 20°C or this is 2 50 night crew At 20°C. So the role or the receptivity will equals 200 times 10 to the power of -8 multiplied by meter because we have the data or the literature value out at 20°C. So in this case, this 18 will be pretty close to 20. So I'm just gonna use 20°C to kind of calculate down this particular problem. So the night cram resisted, the coefficient is also given or known to be 0.000 four degrees Celsius to the power of minus one. And these two are important information for us to be able to actually solve this problem. So next, we want to recall the formula that we want to use. The reason receptivity here is temperature dependent. So when we are actually um increasing the temperature to 75 degrees Celsius, we will need to change and taking account of the temperature difference on the temperature dependent receptivity. So recall that receptivity is a function of temperature where the initial receptivity rose zero or or not will equals 21 plus alpha T minus T zero. Where in this case, our T zero is going to be 20 degrees Celsius and T is going to be 75 degrees Celsius. If you guys are able to find the value for T zero or the resistive itty, not at 18 degrees Celsius. Initially, I feel like it will be better for you guys to use that instead because that will give you guys a more accurate answer. So we're asked for the greatest potential difference recorded over the entire length of the wire. So we asked for the delta fee here. And in this case to calculate delta V, we want to know or we want to use Homes Law. If you recall homes law actually will say that delta V will equals two I or I multiplied by are here. And we know what the I S which is given here. But we are not, no, we do not know what the R is or the resistance. So we need to calculate the resistance. And the greatest potential drop will occurs when the resistance is the greatest. So the greatest are occurs when the temperature is the greatest as well. We want to recall that the calculate our for a long night chrome wire or a long wire, we can calculate it by multiplying the receptivity at a certain temperature multiplied by the length over the actual cross sectional area. And for cylindrical wire which we have here is going to equals to rho L divided by pi R squared just like. So, so resistance increases as temperature goes high. So we want to solve the resistive itty at the T value here of 75 degrees Celsius. But to do so, we want to have to solve order the odd roadie by Ashley taking an account of the temperature difference. So first we want to calculate road at 75 degrees Celsius that will equals two road, not which is going to be this 100 times 10 to the power of minus eight oh multiplied by meter multiply but one plus the alpha value 0.4 degrees Celsius minus one T 75 -20°C. And this will correspond to our role value of roll out at 75 degrees Celsius. The rest of activity of night chrome at 75 degrees Celsius is then going to be 1.22 times 10 to the power of minus six multiplied by meter just like so okay. So next we can actually calculate the resistance by using this formula right here. So our will equals to rho L over pi R squared. So the role is going to be this new role here 1.22 times 10 to the power of minus six multiplied by meter. The L is known to be one m and then the pi R squared is just as always pie. The R is 0.4 times 10 to the power of minus three m. And this will give us squared and this will give us a resistance value of two point oh 33 oh and there we have the resistance. The only thing that's left for us is to actually calculate the greatest potential difference recorded Over the length of the wire by multiplying the amp or the current with the resistance. The current is going to be 0.82 empty. And the resistance is the one that we just found, which is 2.033. And that will correspond to a potential difference value of 1.67 fold. And that will be the answer to our problem. So 1.67 fold will correspond to option B and option B is going to be the answer to this particular practice problem. So if you guys have any sort of confusion on this, please make sure to check out our other lesson videos on similar topics and that will be all for this video. Thank you.

Verified video answer for a similar problem:

Key Concepts

Resistivity and Temperature Dependence

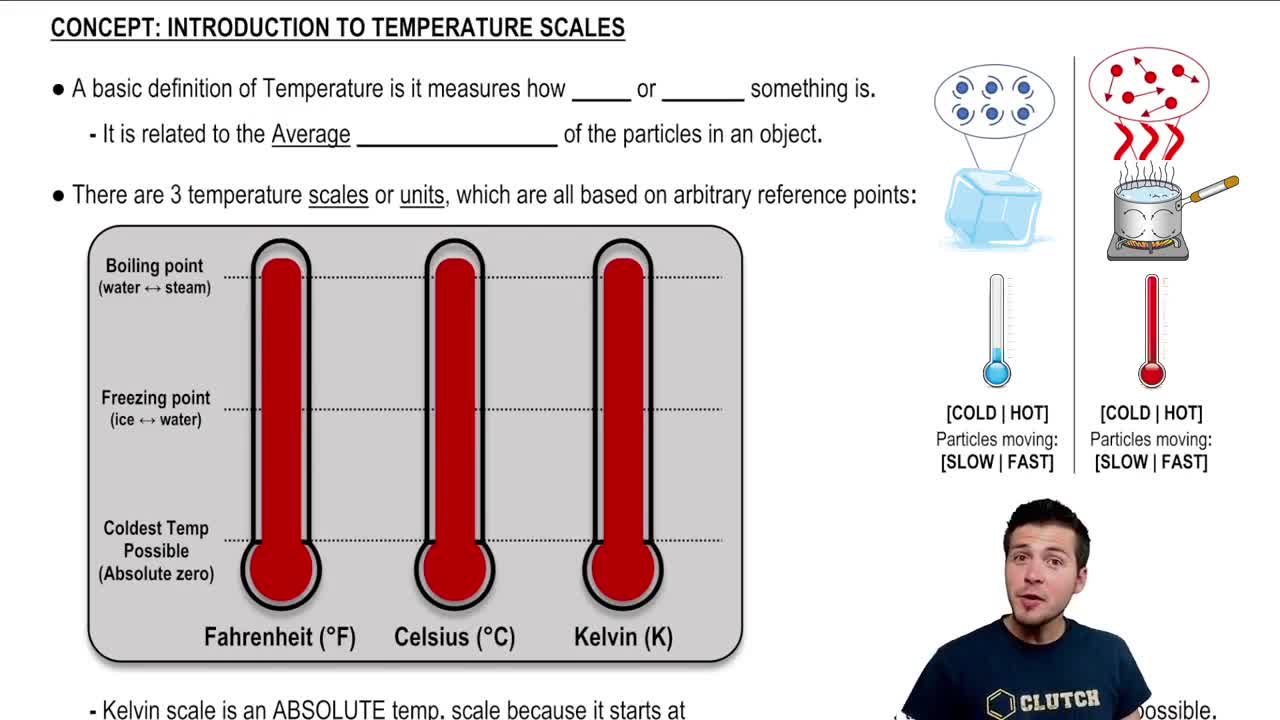
Ohm's Law

Resistance Calculation for Cylindrical Conductors