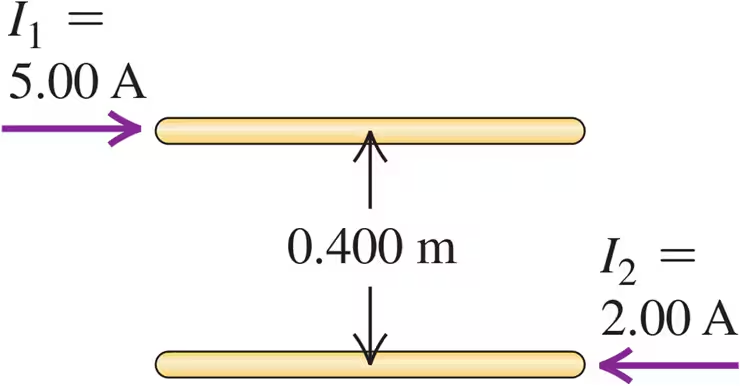
Two long, parallel wires are separated by a distance of 0.400 m (Fig. E28.29). The currents I₁ and I₂ have the directions shown. Each current is doubled, so that I₁ becomes 10.0 A and I₂ becomes 4.00 A. Now what is the magnitude of the force that each wire exerts on a 1.20 m length of the other?

Verified step by step guidance

1. Identify the formula for the magnetic force between two parallel currents: The force per unit length between two parallel wires carrying currents I1 and I2 separated by a distance d is given by the formula: $\frac{\mu o_{0}I{1}_{\hspace{0.17em}}I{2}_{}}{2\pi d}$, where $\mu o_0$ is the permeability of free space.
2. Substitute the given values into the formula: Use the values I1 = 10.0 A, I2 = 4.00 A, and d = 0.400 m. The permeability of free space $\mu o_0$ is approximately $\mathrm{4\pi *10}-7$ T·m/A.
3. Calculate the force per unit length: Plug the values into the formula to find the force per unit length between the wires. This will give you the force in newtons per meter.
4. Determine the total force on a 1.20-m length: Multiply the force per unit length by the length of the wire segment, which is 1.20 m, to find the total force exerted by one wire on the other.
5. Consider the direction of the force: Since the currents are in the same direction, the force will be attractive. Ensure that the direction of the force is consistent with the right-hand rule for magnetic forces.

Key Concepts

Magnetic Force Between Parallel Currents

The magnetic force between two parallel wires carrying currents is determined by the Ampère's force law. The force per unit length between two wires is proportional to the product of the currents and inversely proportional to the distance between them. This concept is crucial for calculating the force exerted when the currents are doubled.

Biot-Savart Law

The Biot-Savart Law describes how currents produce magnetic fields. For a long, straight wire, the magnetic field at a distance from the wire is proportional to the current and inversely proportional to the distance from the wire. Understanding this helps in determining the magnetic field around each wire, which is essential for calculating the force between them.

Superposition Principle

The superposition principle states that the net magnetic field at a point is the vector sum of the magnetic fields produced by each current source independently. This principle is important when considering the effects of both wires on each other, especially when the currents are altered, as it allows for the calculation of the resultant force on each wire.