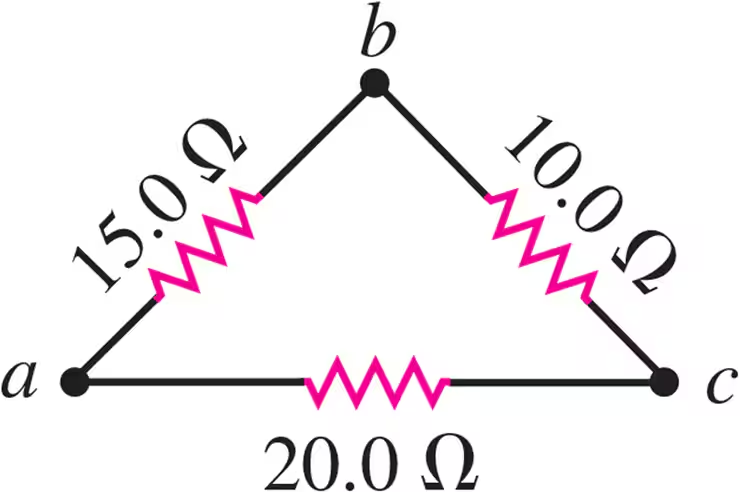
A triangular array of resistors is shown in Fig. E26.5. If the battery has an internal resistance of 3.00Ω, what current will the array draw if the battery is connected across bc?

Verified step by step guidance

1. Identify the resistors in the triangular array. The resistors are labeled as follows: 11.0Ω between points p and s, 13.0Ω between points p and q, and 9.0Ω between points s and r.
2. Determine the configuration of the resistors. The resistors are arranged in a triangular shape, which suggests a combination of series and parallel connections.
3. Calculate the equivalent resistance of the array. First, find the resistance between points p and s (11.0Ω) and between points s and r (9.0Ω) as they are in series. Add these resistances: R_series = 11.0Ω + 9.0Ω = 20.0Ω.
4. Next, consider the parallel connection between the series resistance (20.0Ω) and the resistor between points p and q (13.0Ω). Use the formula for parallel resistances: \( \frac{1}{R_{parallel}} = \frac{1}{R_{series}} + \frac{1}{R_{pq}} \). Substitute the values: \( \frac{1}{R_{parallel}} = \frac{1}{20.0\Omega} + \frac{1}{13.0\Omega} \).
5. Finally, add the internal resistance of the battery (3.00Ω) to the equivalent resistance of the array to find the total resistance. Use Ohm's Law \( I = \frac{V}{R_{total}} \) to calculate the current drawn by the array, where \( R_{total} = R_{parallel} + 3.00\Omega \).

Key Concepts

Ohm's Law

Ohm's Law is a fundamental principle in electronics and physics that relates voltage (V), current (I), and resistance (R) in an electrical circuit. It is expressed as V = IR, indicating that the voltage across a resistor is the product of the current flowing through it and its resistance. This law is essential for calculating the current in a circuit when the voltage and resistance are known.

Series and Parallel Resistor Networks

In electrical circuits, resistors can be arranged in series or parallel configurations. In a series configuration, resistors are connected end-to-end, and the total resistance is the sum of individual resistances. In a parallel configuration, resistors are connected across the same two points, and the total resistance is found using the reciprocal formula: 1/R_total = 1/R1 + 1/R2 + ... + 1/Rn. Understanding these configurations is crucial for analyzing complex resistor networks.

Internal Resistance of a Battery

The internal resistance of a battery is the resistance within the battery that impedes the flow of current. It causes a voltage drop inside the battery, reducing the voltage available to the external circuit. When calculating the current drawn by a circuit, the internal resistance must be considered, as it affects the total resistance and, consequently, the current according to Ohm's Law.