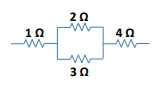
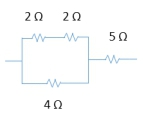
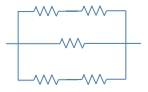
Combining Resistors in Series & Parallel

Hey, guys. So in this video, we're gonna talk about combining resistors, which is a key skill that you have to master for this chapter. Let's go. All right, so in circuit problems, you're often gonna be asked to collapse or combine or merge multiple resistors into a single equivalent resistor single equivalent. Resist store just one. And resistance could be connected to each other in two ways. It could be connected in series or in parallel. And this looks like this in Syria's you're gonna have resistors sort of side by side like this. And parallel, you're gonna have resistors like this. All right? And what you want to do is you want to go from a number of multiple resistors? Let's say here, three into a single equivalent resistor. Same thing here. You wanna turn these three resistors into just a single resistor. Now, what makes this a serious connection is that you have a direct connection between the resisters without any splits in the wire. So imagine if you are a new electron traveling through this wire, you go straight through with no forks on the road. All right, so and then here the wires splits and because the wire splits, you get some loops. So let's say we connect this to let's connect this to a battery toe. A voltage source. Kind of like a battery, right? Remember, charge charge moves out of the current gonna flow out of the positive. The larger terminal here. It's gonna go this way when he gets here, it has the choice of moving this way or this way. So some of the charge will go one way some of the charges go the other way. Eso the wire splits and forms a loop. So one other thing that's important to note is you have a parallel connection whenever you have two resistors that are alone on opposite page on opposite sides on opposite branches. So let me write this alone on opposite branches where opposite sides You can think of it that way as well. So, for example, this guy is alone in this branch. This guy is alone on this branch. So they are alone on opposite sides are on opposite branches. Therefore they are in parallel. All right now, the way you combine them is by using the equivalent resistance equation, which is different for Siris in parallel and you have to memorize this one. The equivalent resistance if you're in Siris is just the addition of the individual resistances R one plus r two plus r three. For example, if this is a one own resistor and this one is too and this one's three, this equivalent resistor here is going to be six. You just add up the numbers Now, if you are in parallel, the equation is a little bit more complicated. It's one over. Our equivalent equals one over R one plus one over r two and you keep adding one of these fractions for each resistor. Here I have three someone, right? One over are three. Okay. And what it means to be an equivalent resistor is that you behave the same as the original group of resistors. So let me illustrate this. Let's connect the battery here positive side of the battery So the current gonna flow out this way. The idea is that this group of resistors, this group of resistors, behaves just as this single resistor would Here, as far as the batteries concern, it is the same exact thing. The battery cannot distinguish these three resistors from a single equipment resistor, which is why they're called equivalents. Same thing here. If you combine these three resistors into a single equivalent resistor, as far as the battery is concerned, the battery sees the same exact amount of resistance. Okay, one last point I want to make is that if you combine resistors in Syria's like we did hear the equivalent resistance we're always going is always going to be higher than the individual resistance is. And this should make sense. Since you're adding the numbers right one plus two plus three, the total number is obviously going to be higher. Now. If you have parallel connection, the number is always going to be lower. And that's because, in this case, remember I mentioned that the the current splits. So now, because the electrons have an option of going one way or the other, there is effectively less resistance because they have a choice co. So let's do two examples here. What is the equipment resistance of the following resistors? What we want to do is get from four resistors into a single resistor, and there are sometimes they're multiple ways of doing this multiple paths that you can take to get to the answer. Sometimes there's only one path, and what you have to sort of do is map about how are you gonna go from 4 to 1? And what you want to do is look for places where you can easily combine these resistors. So, for example, one thing you might do is look at one and start comparing it and start seeing how it's connected to every single one of these. So is one in series or in parallel with two? Well, remember, Siri's means that they have a direct connection. Is there a direct connection from 1 to 2? So if you're if you're a charge, you're going through here and then right here the wire splits. There is no direct connection. So one and two are not in Siris with each other. Okay? They're not in serious. What about in parallel? Well, parallel means that there alone and opposite sides of a branch, they're not even in the same loop. This is a loop. This is a loop. There are different loops, so they're not in parallel either. So you cannot combine one and two right now. What you can do is you can combine one and four because one and four are alone on opposite sides on opposite branches off the loop so you can combine these two in parallel so you can combine these two in parallel. And you can also combine these two in parallel. And if you do that, you go from having 2 to 1, and then you go from having 2 to 1. So now you have a simpler circuit. So let's do that. Let's show that here, I'm gonna go and redraw this where this entire thing is gonna become a single resistor. Let's call this single resistor R one. And over here I'm gonna have another resistor R two. Okay, now how can I get these two guys to be just a single resisted? Well, these guys are in Siris with each other. Hopefully, you see that right away because they're just sitting next to each other. There's no, um, splits on the wire, right? One flows directly to the other. So they are in Siris, which means I'm going to be able to easily combine them into a single resistor. Let's call that are three. So the idea is that everything that's inside of green here becomes just this single resistor right here. So what I like to do is I like to draw the paths without doing the math, get all the way to the end. So I know my path, and then we're now actually going to calculate. Okay, so the first thing I did is I emerged these two into our one. So let's calculate R one r one is in parallel are one is the parallel connection of one and four. So to find our one, I'm gonna have to write the parallel equation, which is this one here. Cool. So it's gonna be one over R one, which is what I'm looking for. And then one over plus one over. I like to make room to plug in variables just so it's a little bit more organized. And then we just gotta plug in the numbers one and +41 And for now, this is a fraction. So you have to get a common denominator, remember, And to get a common denominator between one and four, you could just multiply this side by four. And if you do that in the bottom, have to do at the top and then you can multiply, decided by one, which is effectively not doing anything. And you do the same up here. Now you have four. You have 4/1. I'm sorry. 4/4 plus 1/4. Because the denominators the same. I can combine them into five at the top ads. And the bottom combines 5/4. Are we done? Is that the answer? No. There's one last step which is noticed that the R one isn't the denominators on the bottom of the left side. And I have to solve for R one one way to do this that I like is you can just flip these two. But then if you flip that on the left side, you have to flip on the right side as well. So I'm gonna get one over r one and flip, and I'm gonna get the 5/4 and flip, and it's gonna become 4/5. So our one is 4/5, which is 0.8. Oh, cool. We're gonna do the same thing for eso. We got this guy boom gonna do the same thing to find are 21 over r two equals one over apprentices plus one over apprentices. And this is the This is the parallel connection between the two and the two over here in blue. So we're gonna put a to here and the two year the denominator is already the same. So I'm just gonna merge and say one plus one is to the and then this is one. Now remember, I have to flip this, but here because you have a one. And remember, there's always an implicit one here. If you flip 1/1, you still get a one long story short are too is simply one. Oh, okay. We're almost done. I have war. One I have are two. Now we're just combine them in Siris. Whenever you add something, whatever you combined resistors in Syria's you just add their resistance is so finally are. Three is R one plus R two, which is one plus 10.8, which is 1.8 OEMs. Cool. That's it. That's the final answer for this one. Let's do one more. And what you might want to do here is maybe a positive video and at least lay out the steps off. How would you combine these guys? Okay, I'm gonna keep rolling here. Um, if you if you hopefully you saw right away that these Aaron Siri's with each other and then that these air in series with each other as well, let's color code. You can't merge anything else yet. Okay, So this is going to give me if you follow the wire here carefully, you're gonna go up, and then this entire red thing over here is gonna be replaced by Let's call This guy are one. So that's gonna be our one. And I'm actually gonna make this black. So that's our one. And then down here, the two resistors and blue are gonna become are too. And then once I have these two resistors, hopefully so this isn't seriously is in serious, hopefully see that these guys are in parallel because they're alone on opposite sides on opposite branches of the loop. And I could go one step further and say that these two will just combine into our three. Okay, Now let's calculate r one r two and then our three are one is the Siri's connection. So it's just one plus 21 plus three is four, so I can actually just put it over here. This is four homes. This is two and four, which is six homes. So to find our three, I just have to merge. The four owns with the six homes. So let's do it. Over Here are three one over R three is one over the first resistor, one over the second resistor. In this case, we have a four and a six, So I have a four and a six. The best way to get the easiest way to get a common denominator here is just to multiply this four by six and then put a six on top. And then this six by four, and then put this on top is well, six times four times six is 24 on both of them and on top. I have six plus four, which is 10. So I got 10/24. Are we done? Is that the answer? No. Be careful. You gotta flip the r three. So I'm gonna flip the left and right. So I'm gonna get our 3/1 or just r three equals the flip of these guys. 24 the body by 10 which is just 24 homes and that's the end of this one. Hopefully makes sense. Hopefully you got it. Hope you think it's easy. Let's keep rolling.

Hey, guys. So in this video, I'm gonna show you some awesome shortcuts that you can use in some cases when you have resistors in parallel and this is gonna keep you from having to do a lot of work with fractions, let's check it out. All right, So if you have two resistors in parallel, there's a shortcut equation you can use. Now, remember, the general equation is that the equivalent resistance in parallel is one over our equivalents equals to one over R one plus one over R To this is if you have two resistors, this is the general equation, okay? And I'm gonna solve for our equivalents so that you never have to do this again. And you could just use a shortcut if you have two resistors, which is the most common thing you're gonna get. So the first thing if you remember we have to do is get a common denominator. And to do that, you're just gonna multiply our to here and then multiply our one here. So are one times are too. So if I do in the bottom, I also have to do in the top or two, and then are two times are one times are one. Let's extend the little fraction thing. So what happens now is I have are one or two in the bottom are one or two in the bottom. So I have a common denominator. So I can write our one times are too. And then at the top I have are two plus are one or I'm gonna ride R one plus R two. So it's in order. Are we done Know? Remember, we have to flip the sides. So if I flip here, I get our equivalents over one or simply are equivalent equals. And then if I flip the left, I gotta flip the right and this is gonna look, I'm sorry. This was a two right there. Hopefully caught that are one times are too over our one plus our two now notice. I'm drawing the r one and r two in the bottom really far apart. And the reason I'm doing this is because one of the biggest problems with this equation is that people forget whether the times is on top or the pluses on top. You dont know what goes where you might forget the way I remember which is silly but works is because this is a dots. It's a tiny dots. The R one r two are really close together, and this is a fat plus sign, which takes up a lot more space. The bottom variables are farther apart, and the skinny top and fat bottom gives you sort of a triangle. Okay, super silly. But maybe hopefully it works for you. Whatever works, right? So that's the equation. So whenever you have two resistors in parallel, you can just use that equation instead of playing with fractions. Okay, Now, super important is that you cannot do this for three or more resistors, so I actually want you to draw right This here. This is wrong, but I want you to write it. Let's say you might want to think that you can multiply are one or two. Why not just add an R three here and then at the bottom here, do a plus R three. Well, this is wrong. This does not work. So I want you to write it, scratch it out and say, Don't okay, do not do this. This Onley works for two resistors. It does not work for more than two. Okay, eso let me give you a super quick example here. Let's say you have a four and a six, and you want to combine them into a single resistor. You would just use this equation here and say that the equivalent resistance is four times six, divided by four plus six. I'm setting up the apprentices so I can put the numbers inside +4646 And this is 24 divided by 2.4, right, much faster than play with fractions. So that's the first shortcut. Um, the most important thing always is that you know the general equation, because this is gonna work for everything. But the shortcut is pretty handy as well. It's more important to shortcut number two, but shortcut number two is super simple. If you have resistors of the same resistance, you can also use a shortcut equation. So let's say I have a Let's make it creepy. 66 and six. Let's say you have something like this. What's the equivalent resistance? Well, if you write the the general equation, remember, you cannot write this equation right here. The one we just talked about because that works only for two. But if you have this, you end up with something like this 1/6, plus 1/6, plus 1/6. And the denominators already the same to end up with 3/6 or 6/3, which is to the fast way to have done this is to just say that the equivalent resistance when they're all the same in parallel is just the same resistance which in this case, is six divided by the number of resistors. So you could have just done six divided by three is too. For example, if you have eight, eight, eight, and eight the equivalent resistance here his super easy to calculate its AIDS and there are four of them. The equivalent resistance is just a to cool. So now I'm gonna do an example. That sort of merges all these ideas. You not know how to easily combine things that are the same. And you know how to easily combine when they're the same resistance and you know how to easily combine. If there's two of them using that first equation now, you can actually use those two rules to your advantage. So if you get a question like this. This might look Harry, but it's actually really simple. So we're going to do notice we have a nine a nine in the nine. And even though they're not right next to each other, you could technically rearrange them to be right next to each other. And you can say, You know what? This nine with this nine and this nine because they're the same, I can write. The equivalent resistance of the three nines is just 9/3. I'm using this shortcut right here. There are three nines, so it's just nine divided by three, which is three. Okay, you can do the same thing for the 12. There's 2 12 so I can say the equivalent resistance of the combined are gonna be 12 divided by two just six. So what I can do is all the Reds become a simple a single three and the and the blue becomes a six. And now, if I combine these two because I have two resistors that are parallel to each other, right, let's put the little connectors this way. So there's two resistors here. There are parallel to each other. I can use the first shortcut equation, which is You multiply at the top and then you add at the bottom. Remember the pyramid, right? It's multiply, um, and add. So this is gonna be three times 63 plus times six, of course, is 18 3 divided three plus six is nine. Silly answer here is to homes. So notice how we're able to combine everything really, really quickly. 1993 12 12 is a six. Put them together and you get a two. All right, that's it for this one. Let's get going.

Hey, guys. So in this video, I want to go over an example of a network of resistors that looks scarier than it really is. So here we want to find the equivalent resistor of these guys, and it looks really Harry, but I want to show you how you can make it look more familiar to solve this question. Okay. And that you think we're gonna do here, is we're gonna move the wires around, um, so that they look more familiar. So, for example, um, the five and the four are sort of at an angle, which is unusual. And it doesn't. It makes it harder to sort of visualize what's really going on here. So the first thing I'm gonna do is I'm gonna try to make this four vertical, and I can actually just move this point here where the three of them three wires touch. I can move this point right here and then imagine if you have a four and then you're grabbing the bottom right? You're grabbing the bottom and just doing this, Okay? So if I do that, let's redraw. I'm gonna get a two at the top. That's three here and then this red point right here is now going to be rights here so that I get a four like this. And then there's still a five here. Let's leave that alone. Will take this slowly. And now this hopefully looks, um, mawr familiar. The other thing we could do is notice that this is a single branch right here. That's all along this green line. There are no points where the wire splits. Now, obviously, the wire splits here in the green dot splits in the red dot But within those two dots, nothing splits. What that means is that you can actually move the three and just redraw the three over here. And it is exactly the same thing. Functions just the same. So now we get something a little cleaner, and I'm gonna draw again. I'm going really slowly because I wanna make sure you fully understand this. Okay? And now it looks like this, and hopefully now this looks super familiar. Hopefully you'll see that this is a branch with a single resistor in it. And this is a branch here also with a single resistor on it or in it. And because you have two resistors on opposite sides there, alone on opposite sides of this loop. Here they are in parallel. So these two guys are in parallel so I can combine them. Okay, Usually I would keep going, but just just for the sake of just getting this over with, let's just combine these two real quick. And because I have two resistors in parallel, I can use the shortcut equation. The equipment resistance is going to be Remember the pyramid? It's times on top and plus on the bottom. Okay, so it's gonna be four times three, divided by four plus three. This is 12 divided by seven, which is one 17 So this entire thing can be redrawn as a. This whole thing here actually can think of it as all of this can be redrawn. There's a two, there's a five, and instead of having a four and then the three, I'm just gonna have a single 1.7 right here and now this is a little simpler because I have three instead of two. Now, what about this other five here? I fixed the four, made it straight. Let's make the five straight and the five like this. So I'm gonna move the top a little bit, and then I'm gonna move the bottom a little bit so really slowly here, the five is gonna be moved over here, and this part of the five is gonna be moved over here so that it forms sort of a straight line, and this is going to look like this. Got a true and then you got a five straight down, and then there's still the the seven over here. Now the seven sort of like this, right? If you curve the the seven is kind of like, straight like this, the 1.7 rather. But I could extend this wire and make it look like this. Okay. All these air equivalent, you just have to be careful to redraw them correctly. Otherwise, you made up a new circuit, and obviously it's gonna be wrong. Okay. Again. Here. Hopefully you see that you have a branch with a single resistor. And then here you have a branch with a single resistor. And because you have two resistors that alone on their branches on their opposite sides, they are also in parallel. And once again, I can use the parallel shortcut equation. Because I have two resistors. The equipment resistance is going to be five times 1.7, divided by five plus 1.7. And if you do this in the calculator, you get 1. 1.3. I want to quickly remind you of something that we talked about earlier, which is whenever you combine things in parallel, the total resistance is smaller or lower than the all of the resistance is. So it's gonna be lower than the five. And it's gonna be lower than the 1.7 notice that when I emerged them, I got a 1.3 lower than 1.7. It makes sense. You can use that to validate that. You're probably correct. So finally here, I can draw the two, and in this entire thing here gets replaced. Instead of there being two of them, there's gonna be just a single 1.3. And these are the points, um, that we have there now notice that between these two guys there's a direct connection between them. There's no forks between them, which means that they are in Siris and finally, serious resistors are just added um s 02 plus 1.3 is 3.3. So the equivalent resistance of that big old mess is just 3.3 OEMs. So please do know that you can take the liberty to move some wires around to make things look more familiar to you. Different people see things a little bit differently, and they prefer their resistance to be organized differently in the book Might throw you book. A professor might throw you some some questions that are drawn in a weird way to see if you really know what's going on. Take some liberty to draw them, but please make sure they do it correctly. Cope. That's it for this one. Let's get going.