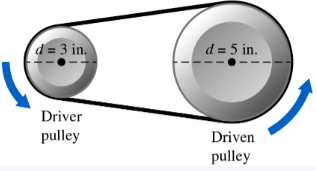
Solve each problem. The speed of a pulley varies inversely as its diameter. One kind of pulley, with diameter 3 in., turns at 150 revolutions per minute. Find the speed of a similar pulley with diameter 5 in.

Verified step by step guidance

1. Identify the type of variation described: the speed \( S \) varies inversely as the diameter \( D \). This means the relationship can be written as \( S = \frac{k}{D} \), where \( k \) is a constant.
2. Use the given values to find the constant \( k \). Substitute \( S = 150 \) revolutions per minute and \( D = 3 \) inches into the equation \( 150 = \frac{k}{3} \).
3. Solve for \( k \) by multiplying both sides of the equation by 3, giving \( k = 150 \times 3 \).
4. Write the general formula for speed using the constant \( k \): \( S = \frac{k}{D} \).
5. Find the speed of the pulley with diameter 5 inches by substituting \( D = 5 \) into the formula: \( S = \frac{k}{5} \).

Key Concepts

Inverse Variation

Inverse variation describes a relationship where one quantity increases as the other decreases, such that their product is constant. In this problem, speed varies inversely with diameter, meaning speed × diameter = constant.

Setting up the Variation Equation

To solve inverse variation problems, express the relationship as speed × diameter = k, where k is a constant. Use known values to find k, then apply it to find the unknown speed for the new diameter.

Solving for Unknowns in Variation Problems

After determining the constant of variation, substitute the new diameter into the equation and solve for the unknown speed. This step involves basic algebraic manipulation to isolate and calculate the desired value.