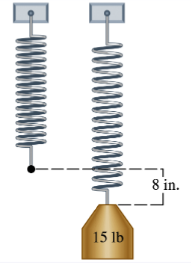
Hooke's Law for a Spring Hooke's law for an elastic spring states that the distance a spring stretches varies directly as the force applied. If a force of 15 lb stretches a certain spring 8 in., how much will a force of 30 lb stretch the spring?

Verified step by step guidance

1. Identify the relationship given by Hooke's Law: the distance stretched \(d\) varies directly as the force applied \(F\). This can be written as \(d = kF\), where \(k\) is the constant of proportionality.
2. Use the given information to find the constant \(k\). Substitute \(F = 15\) lb and \(d = 8\) in. into the equation \(d = kF\) to get \(8 = k \times 15\).
3. Solve for \(k\) by dividing both sides of the equation by 15: \(k = \frac{8}{15}\).
4. Use the constant \(k\) to find the new distance stretched when the force is 30 lb. Substitute \(F = 30\) and \(k = \frac{8}{15}\) into \(d = kF\) to get \(d = \frac{8}{15} \times 30\).
5. Simplify the expression to find the distance \(d\) the spring stretches under a 30 lb force.

Key Concepts

Direct Variation

Direct variation means one quantity changes proportionally with another. In this problem, the distance the spring stretches varies directly with the applied force, so if the force doubles, the stretch doubles. This relationship can be expressed as y = kx, where k is a constant.

Hooke's Law

Hooke's Law states that the force needed to stretch or compress a spring is proportional to the displacement from its rest position. Mathematically, F = kx, where F is force, x is displacement, and k is the spring constant. This law applies within the elastic limit of the spring.

Solving Proportions

Solving proportions involves setting two ratios equal to each other to find an unknown value. Here, the ratio of force to stretch length is constant, so you can set up the proportion 15/8 = 30/x and solve for x to find the new stretch length.