Textbook Question
(a) Draw a picture that represents a crystalline solid at the atomic level.
927
views


 Verified step by step guidance
Verified step by step guidance

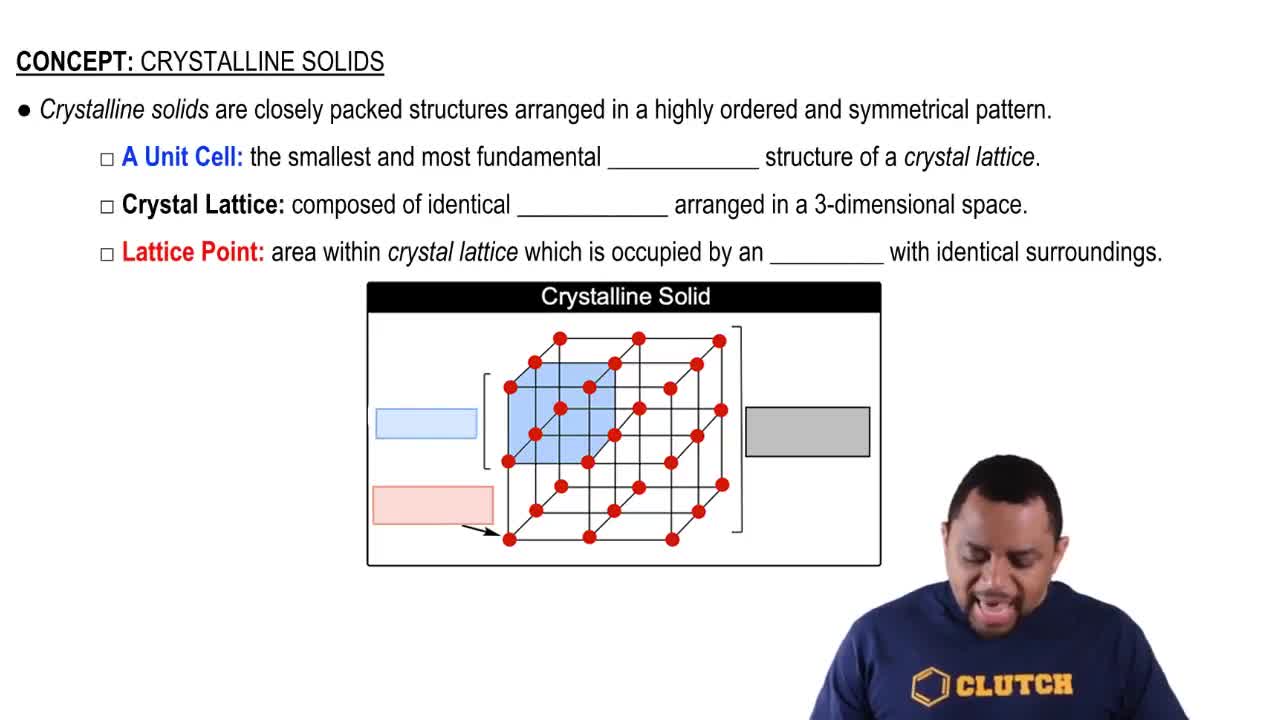
(a) Draw a picture that represents a crystalline solid at the atomic level.
(b) Now draw a picture that represents an amorphous solid at the atomic level.
Two patterns of packing two different circles of the same size are shown here. For each structure (c) determine the type of two-dimensional lattice (from Figure 12.4). (i)
(ii)
Imagine the primitive cubic lattice. Now imagine grabbing the top of it and stretching it straight up. All angles remain 90. What kind of primitive lattice have you made?
Which of the three-dimensional primitive lattices has a unit cell where none of the internal angles is 90? (a) Orthorhombic, (b) hexagonal, (c) rhombohedral, (d) triclinic, (e) both rhombohedral and triclinic.