A car starts from rest at a stop sign. It accelerates at 4.0 m/s² for 6.0 s, coasts for 2.0 s, and then slows down at a rate of 3.0 m/s² for the next stop sign. How far apart are the stop signs?

A 1000 kg weather rocket is launched straight up. The rocket motor provides a constant acceleration for 16 s, then the motor stops. The rocket altitude 20 s after launch is 5100 m. You can ignore any effects of air resistance. What was the rocket's acceleration during the first 16 s?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
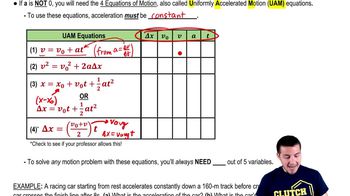
Newton's Second Law of Motion

Kinematic Equations
Free Fall and Gravity

A cheetah spots a Thomson's gazelle, its preferred prey, and leaps into action, quickly accelerating to its top speed of 30 m/s, the highest of any land animal. However, a cheetah can maintain this extreme speed for only 15 s before having to let up. The cheetah is 170 m from the gazelle as it reaches top speed, and the gazelle sees the cheetah at just this instant. With negligible reaction time, the gazelle heads directly away from the cheetah, accelerating at 4.6 m/s² for 5.0 s, then running at constant speed. Does the gazelle escape? If so, by what distance is the gazelle in front when the cheetah gives up?
Find an expression for the minimum stopping distance dstop of a car traveling at speed v0 if the driver's reaction time is Treact and the magnitude of the acceleration during maximum braking is a constant abrake.
A 200 kg weather rocket is loaded with 100 kg of fuel and fired straight up. It accelerates upward at 30 m/s² for 30 s, then runs out of fuel. Ignore any air resistance effects. What is the rocket's maximum altitude?
A lead ball is dropped into a lake from a diving board 5.0 m above the water. After entering the water, it sinks to the bottom with a constant velocity equal to the velocity with which it hit the water. The ball reaches the bottom 3.0 s after it is released. How deep is the lake?
A hotel elevator ascends 200 m with a maximum speed of 5.0 m/s. Its acceleration and deceleration both have a magnitude of 1.0 m/s2. How long does it take to make the complete trip from bottom to top?
