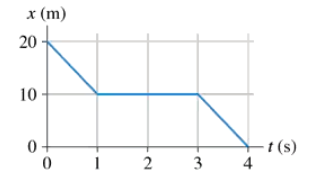
FIGURE EX2.5 shows the position graph of a particle. Draw the particle’s velocity graph for the interval .

Question

Accepted Answer

Welcome back everyone. In this problem, the position time graph of a moving vehicle is shown below. What will the velocity time graph of the vehicle look like? For the given interval? On our right, we have our position time graph. Let me highlight that here. And on our left, we have an empty graph that we're supposed to make our velocity time graph. Now how are we going to create our velocity time graph? Well, the name says it all, it's going to be a plot of our velocity over time in our position time graph. It's a plot of our distance over time where our vertical axis represents the distance and our horizontal axis represents our time. Now we can model the object as a particle so that it has one well defined position. Notice from our position time graph, it tells us the motion is in the X direction. So the velocity we determine will be the X component of the velocity. What do we know about velocity? Well, recall that velocity is equal to the change in distance over time. So in this case, this will be equal to the change in distance X over the change in time T. And as we said, it will be the velocity of our X component. If you notice on our position time graph, there are three distinct periods in our graph. First notice that from 0 to 10 seconds, our time is increasing or sorry or distance is increasing next from 10 to 25 seconds, our distance stays the same. And from 25 to 30 seconds, our distance is decreasing. So if we can find the velocity at these three periods, then we should be able to plot our velocity time graph. So let's go ahead and do that. Let's start from zero seconds to 10 seconds. What's our velocity going to be? Well, no, it's going to be the difference or the change in distance. Sorry. So that's going to be 150 m minus 0 m divided by our change in time, which is 10 seconds minus zero seconds. That's 150 m divided by 10 seconds, which makes it 15 m per second. Now, if we go to our velocity time graph here, I'm going to put each interval or each increment in fifteens. In other words, 1530 so on and down words that's negative 15, negative 30 so on. OK. And now we are going to put over 15 m per second from 0 to 10 seconds on our velocity time graph. So it would look something like this next. Let's look at what happens from 10 to 25 seconds. So let me write it a bit below here. No, from 10 to 25 seconds, like we said, you can notice that our distance has not changed. Ok? So a change in distance is going to be 0 m and our change in time is gonna be 25 seconds minus 10 seconds. 25 minus 10 equals 15 and 0 m divided by 15 seconds equals 0 m per second. Ok? So no, from 10 to 25 seconds, our velocity is 0 m per second. So if we go back to our diagram again, we'll go to a velocity of 0 m per second from 10 to 25 seconds. And I apologize. My lines aren't too straight. Ok? They're, they're a bit uh distorted here, but I'm trying to draw them as best as I can. So I think that looks, OK? And just to show here that this is our change now we're on to the final part of our position time graph from 25 to 30 seconds. So from 25 seconds to 30 seconds. No, we know that our distance has gone from 150 m to 0 m. So that's gonna be 0 m minus 150 m divided by 30 seconds minus 25 seconds. Zero minus 150 equals negative 150 30 minus 25 equals five and negative 150 m divided by five seconds equals negative 30 m per second. So from 25 to 30 seconds, our speed is negative 30 m per second. So again, we can represent that on our diagram, know that we've put all of our velocities on our velocity time graph. This is going to be the velocity time graph for our position. Sorry for our given interval. Thanks for watching everyone. I hope this video helped.

FIGURE EX2.5 shows the position graph of a particle. Draw the particle’s velocity graph for the interval .

Verified video answer for a similar problem:

Key Concepts

Position vs. Time Graphs

Velocity

Graphical Interpretation