Textbook Question
Let E = 2i + 3j and F = 2i - 2j. Find the magnitude of E and F.
1255
views

 Verified step by step guidance
Verified step by step guidance


Let E = 2i + 3j and F = 2i - 2j. Find the magnitude of E and F.
Let E = 2i + 3j and F = 2i - 2j. Find the magnitude of -E - 2F.
FIGURE EX3.19 shows vectors A and B. What is C = A + B? Write your answer in component form using unit vectors.
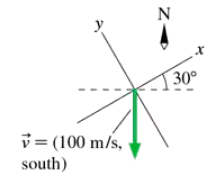
Let = (5.0 m, 30 degrees counterclockwise from vertically up). Find the x- and y-components of in each of the two coordinate systems shown in FIGURE EX3.21.
Let , and . Find the magnitude and the direction of .
The position of a particle as a function of time is given by = ( 5.0î +4.0ĵ )t² m where t is in seconds. What is the particle's distance from the origin at t = 0, 2, and 5 s?