Textbook Question
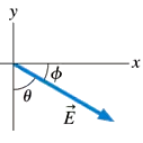
Trace the vectors in FIGURE EX3.1 onto your paper. Then find .
1215
views

 Verified step by step guidance
Verified step by step guidance

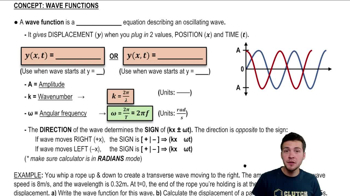

Trace the vectors in FIGURE EX3.1 onto your paper. Then find .
Trace the vectors in FIGURE EX3.1 onto your paper. Then find .
A velocity vector 40 degrees below the positive x-axis has a y-component of -10 m/s. What is the value of its x-component?
A position vector in the first quadrant has an x-component of 6 m and a magnitude of 10 m. What is the value of its y-component?
Draw each of the following vectors. Then find its x- and y-components.