FIGURE EX4.36 shows the angular velocity graph of the crankshaft in a car. What is the crankshaft's angular acceleration at t = 3s

Question

Accepted Answer

Hey, everyone in this problem, we have a periodic varying force that acts on a shaft. The graph below shows the angular velocity of the shaft. And we're asked to find the angular acceleration at T equals eight seconds. Hm. Now looking at this diagram, OK, we were given time t in seconds on the X axis omega the angular speed and radiance per second on the Y axis. And we have these linear segments. OK. So we have 1234 linear segments in this graph, we're given four answer choices, options A through D all in radiance per second squared. Option A is negative 33.3, option B negative 40 option C negative option D 33.3. Now we're asked to find the angular acceleration. OK. And let's recall the relationship between angular acceleration that we're looking for and the angular velocity that we're given. OK. And that's the same relationship as in the linear case. So the angular acceleration alpha, it's gonna be equal to D omega divided by D T. Hey, it's the derivative of the angular velocity with respect to time. Now, when we're given the graph of the angular velocity. How do we find the derivative? OK. Well, on the graph, the derivative is just going to be the slope. So we are looking for the slope of our angular velocity curve. Now we're interested at T equals eight seconds. So at T equals eight seconds. OK. Omega the curve for Omega is a linear, right. How do we find the solo of a linear curve? Well, this is just going to be rise over run. OK. So alpha, our angular acceleration is gonna be the change in Omega, the angular velocity divided by the change in time in this particular section. OK. And again, we're interested at T equals eight seconds. And so we're gonna take this entire segment from six seconds to 12 seconds because again, we have a straight line, it's linear, it's gonna have the same slope as that T equals eight seconds over that whole interval. So the change in Omega is gonna be the final angular velocity minus the initial angular velocity Omega F minus Omega not minus the final or sorry, divided by the final time minus the initial time. Now, the final angular velocity is gonna be the angular velocity at seconds, which is 200 radiant per second. So we have 200 radiant per second minus the initial angular speed or velocity which is at six secondss, 400 radiance per second. And then we divide by the difference in time, 12 seconds minus six seconds. OK. So we're calculating rise over run for the segment from six seconds to 12 seconds. Now working this out in the numerator, we have negative 200 radiant per second and that is gonna be divided by six seconds, which is gonna give you an angular acceleration alpha of negative 33.33 radiance per second squared. And this negative value makes sense. OK. Looking at our graph, we can see that the slope is negative. OK. This line is going downwards. So we expect that that acceleration is going to be negative in order to slow down our speed. And so the correct answer here is option a negative 33.3 radiance per second squared. That's it for this one. Thanks everyone for watching. See you in the next video.

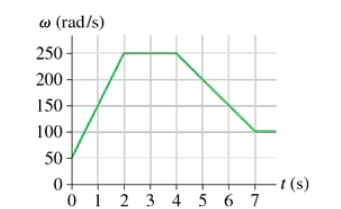
FIGURE EX4.36 shows the angular velocity graph of the crankshaft in a car. What is the crankshaft's angular acceleration at t = 3s

Verified video answer for a similar problem:

Key Concepts

Angular Velocity

Angular Acceleration

Graph Interpretation