A jet plane is speeding down the runway during takeoff. Air resistance is not negligible. Identify the forces on the jet.

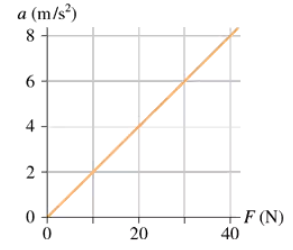
FIGURE EX5.14 shows an object's acceleration-versus-force graph. What is the object's mass?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Newton's Second Law of Motion

Force-Acceleration Graph
Slope of a Line

FIGURE EX5.8 shows an acceleration-versus-force graph for three objects pulled by rubber bands. The mass of object B is 0.20 kg. What are the masses of objects A and C? Explain your reasoning.
For an object starting from rest and accelerating with constant acceleration, distance traveled is proportional to the square of the time. If an object travels 2.0 furlongs in the first 2.0 s, how far will it travel in the first 4.0 s?
What is the acceleration, as a multiple of g, if this force is applied to a 110 kg bicyclist? This is the combined mass of the cyclist and the bike.
Newton's First Law Exercises 17, 18, and 19 show two of the three forces acting on an object in equilibrium. Redraw the diagram, showing all three forces. Label the third force F3.
Newton's First Law Exercises 17, 18, and 19 show two of the three forces acting on an object in equilibrium. Redraw the diagram, showing all three forces. Label the third force F3.
