Skip to main content
Pearson+ LogoPearson+ Logo
Ch 06: Dynamics I: Motion Along a Line
Knight Calc - Physics for Scientists and Engineers 5th Edition
Knight Calc5th EditionPhysics for Scientists and EngineersISBN: 9780137344796Not the one you use?Change textbook
All textbooksKnight Calc 5th EditionCh 06: Dynamics I: Motion Along a LineProblem 40a
Chapter 6, Problem 40a

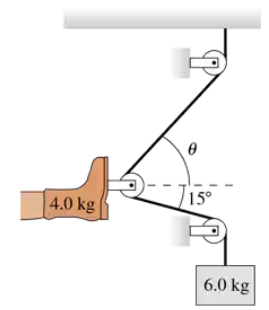
An accident victim with a broken leg is being placed in traction. The patient wears a special boot with a pulley attached to the sole. The foot and boot together have a mass of 4.0 kg, and the doctor has decided to hang a 6.0 kg mass from the rope. The boot is held suspended by the ropes, as shown in FIGURE P6.40, and does not touch the bed. Determine the amount of tension in the rope by using Newton's laws to analyze the hanging mass. Hint: If the pulleys are frictionless, which we will assume, the tension in the rope is constant from one end to the other.

Verified step by step guidance
1
Step 1: Analyze the forces acting on the hanging mass. The mass is 6.0 kg, and the force due to gravity acting on it is given by F = m * g, where m is the mass and g is the acceleration due to gravity (approximately 9.8 m/s²). This force is the weight of the mass.
Step 2: Recognize that the tension in the rope is constant throughout because the pulleys are frictionless. This means the tension in the rope supporting the hanging mass is the same as the tension in the rope connected to the boot.
Step 3: Apply Newton's second law to the hanging mass. Since the mass is stationary, the net force acting on it is zero. Therefore, the upward tension in the rope must equal the downward gravitational force acting on the mass.
Step 4: Write the equation for equilibrium: T = m * g, where T is the tension in the rope, m is the mass of the hanging object (6.0 kg), and g is the acceleration due to gravity (9.8 m/s²). Substitute the values into the equation to find the tension.
Step 5: Interpret the result. The tension calculated in the previous step is the same throughout the rope, including the section holding the boot. This tension is responsible for keeping the boot suspended in equilibrium.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
1m
Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Newton's Laws of Motion

Newton's Laws of Motion describe the relationship between the motion of an object and the forces acting on it. The first law states that an object at rest will remain at rest unless acted upon by a net external force. The second law quantifies this relationship, stating that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F=ma). The third law states that for every action, there is an equal and opposite reaction.
Recommended video:
Guided course
04:46
Newton's 1st Law

Tension in a Rope

Tension is the force transmitted through a rope or string when it is pulled tight by forces acting from opposite ends. In a frictionless pulley system, the tension is constant throughout the rope. This means that the tension acting on the hanging mass is equal to the weight of the mass minus any other forces acting on the system, such as the weight of the boot in this scenario.
Recommended video:
Guided course
06:34
Calculating Tension in a Pendulum with Energy Conservation

Equilibrium of Forces

An object is in equilibrium when the net force acting on it is zero, meaning all forces are balanced. In the context of the traction system, the forces acting on the boot and the hanging mass must balance out. This involves considering the gravitational force acting on the masses and the tension in the rope, allowing us to set up equations to solve for unknowns, such as the tension in the rope.
Recommended video:
Guided course
05:10
Equilibrium
Related Practice
Textbook Question

So-called volcanic 'ash' is actually finely pulverized rock blown high into the atmosphere. A typical ash particle is a 50-μm\mu m-diameter piece of silica with a density of 2400 kg/m3. How long in hours does it take this ash particle to fall from a height of 5.0 km in still air? Use the properties of 20°C air at sea level.

1563
views
1
comments
Textbook Question

An E. coli bacterium can be modeled as a 0.50 μm diameter sphere that has the density of water. Rotating flagella propel a bacterium through 40°C water with a force of 65 fN, where 1 fN = 1femtonewton = 10-15 N. What is the bacterium's speed in μm/s?

702
views
Textbook Question

A 2.0 kg object initially at rest at the origin is subjected to the time-varying force shown in FIGURE P6.38. What is the object's velocity at t = 4 s?

138
views
Textbook Question

Seat belts and air bags save lives by reducing the forces exerted on the driver and passengers in an automobile collision. Cars are designed with a 'crumple zone' in the front of the car. In the event of an impact, the passenger compartment decelerates over a distance of about 1 m as the front of the car crumples. An occupant restrained by seat belts and air bags decelerates with the car. By contrast, an unrestrained occupant keeps moving forward with no loss of speed (Newton's first law!) until hitting the dashboard or windshield. These are unyielding surfaces, and the unfortunate occupant then decelerates over a distance of only about 5 mm. A 60 kg person is in a head-on collision. The car's speed at impact is 15 m/s. Estimate the net force on the person if he or she is wearing a seat belt and if the air bag deploys.

106
views
Textbook Question

Compressed air is used to fire a 50 g ball vertically upward from a 1.0-m-tall tube. The air exerts an upward force of 2.0 N on the ball as long as it is in the tube. How high does the ball go above the top of the tube? Neglect air resistance.

1007
views
Textbook Question

A rifle with a barrel length of 60 cm fires a 10 g bullet with a horizontal speed of 400 m/s. The bullet strikes a block of wood and penetrates to a depth of 12 cm. How long does it take the bullet to come to rest?

1312
views