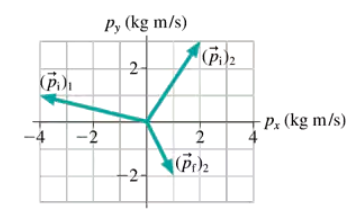
Two objects collide and bounce apart. FIGURE EX11.31 shows the initial momenta of both and the final momentum of object 2. What is the final momentum of object 1? Write your answer using unit vectors.

Verified step by step guidance

1. Step 1: Identify the given information from the graph. The initial momentum of object A (pA,i) and object B (pB,i) are shown as vectors, along with the final momentum of object B (pB,f). The task is to find the final momentum of object A (pA,f).
2. Step 2: Apply the principle of conservation of momentum. The total momentum before the collision must equal the total momentum after the collision. Mathematically, this is expressed as: $p$_A,i + p_B,i = p_A,f + p_B,f.
3. Step 3: Break the momentum vectors into their x and y components. From the graph: $p$_A,i = (2, 2), $p$_B,i = (-1, 1), and $p$_B,f = (1, 1). Use these values to calculate the components of $p$_A,f.
4. Step 4: Solve for the x-component of $p$_A,f. Using conservation of momentum in the x-direction: $p$_A,i,x + p_B,i,x = p_A,f,x + p_B,f,x. Substitute the values: $2\; +\; (-1)\; =\; p$_A,f,x + 1. Solve for $p$_A,f,x.
5. Step 5: Solve for the y-component of $p$_A,f. Using conservation of momentum in the y-direction: $p$_A,i,y + p_B,i,y = p_A,f,y + p_B,f,y. Substitute the values: $2\; +\; 1\; =\; p$_A,f,y + 1. Solve for $p$_A,f,y.

Key Concepts

Momentum

Momentum is a vector quantity defined as the product of an object's mass and its velocity. It is represented as p = mv, where p is momentum, m is mass, and v is velocity. In collisions, momentum is conserved, meaning the total momentum before the collision equals the total momentum after the collision, provided no external forces act on the system.

Vector Addition

Vector addition is the process of combining two or more vectors to determine a resultant vector. In the context of momentum, this involves adding the momentum vectors of the colliding objects. The components of the vectors are added separately in the x and y directions, allowing for the calculation of the final momentum of each object after the collision.

Elastic Collision

An elastic collision is a type of collision where both momentum and kinetic energy are conserved. In such collisions, the objects bounce off each other without any loss of kinetic energy. This is in contrast to inelastic collisions, where kinetic energy is not conserved. Understanding the nature of the collision is crucial for applying the conservation laws correctly to find the final momenta of the objects involved.