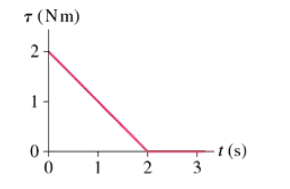
An object whose moment of inertia is 4.0 kg m^2 is rotating with angular velocity 0.25 rad/s. It then experiences the torque shown in FIGURE EX12.25. What is the object's angular velocity at t = 3.0s?

Video transcript

Hi, everyone in this practice problem, we're being asked to find the angular velocity of a bar at T equals 2.5 seconds. We will be given a bar with a moment of inertia of 3.5 kg meters squared spinning on its axis at an initial angular velocity of 1. radiant per seconds. We are also given an image showing the torque versus the time applied to the bar where at T equals zero seconds, the torque will be at four Newton meter and at P equals one seconds, the torque will go down up until P equals 2.5 seconds. When the torque will reach zero Newton meter, we're being asked to find the angular velocity of the bar at D equals 2. seconds. And the options given are a 2. radiance per seconds. B 0.7 radiance per seconds, C 3.3 radiant per seconds. D 6.3 radium per seconds and E 1.3 radiance per seconds. Awesome. So the angular acceleration is going to be given by alpha. So alpha will equals to the torque or tau divided by the moment of inertia or I so alpha is going to be the angular acceleration tau is going to be the torque and I is going to be the moment of inertia. This actually implies that the graphs shown or the picture given for torque versus time will imply that the graph of the angular acceleration is actually also going to be the same as this Tau versus time graph having the numerical values all divided by an I because in this case, the I is also or the I, the moment of inertia is just a constant value. So the shape of the angular X, the graph of the angular acceleration will be exactly the same as the Tau or the torque having the numerical values all divided by an I. The rotational kinematic equation that we're going to use in this case is then going to equals to omega F equals omega I plus A where omega F is the final angular velocity omega I is the initial angular velocity. And the A is going to be the area under the angular acceleration curve from P equals T I to T equals T F. In our case T I is going to equals to zero seconds and T F is going to be the time what the time that we are interested in finding, which is T equals 2.5 seconds. Awesome. It is given in the uh in the problem statement that the initial angular velocity is going to equals to 1.3 radiance per second. And the moment of inertia I is given to be 3.5 kg meter squared just like. So the area under the curve between P equals zero seconds and T equals 2.5 seconds is still unknown, which is a and that is what we're going to find first in order for us to eventually find the final angular velocity at P equals 2.5 seconds. So the area under the curve A between T equals zero and P equals 2.5 seconds will equals to B, the area of the rectangle here from T equals zero seconds to T equals one seconds plus the area of the triangle from T equals one seconds to T equals 2.5 seconds. So A equals area of rectangle. We wanna plus that with the area of the triangle. OK. So let's start with the area of the rectangle, the area of the rectangle from T equals 0 to 1 second. Well, equals to B, one seconds, which is going to be the length, one seconds multiplied that by the width which is going to be four Newton meter just like. So, and then the area of the triangle is going to be half multiplied by the base of the triangle, which is going to be from one seconds to 2.5 seconds. So that will actually be 1.5 seconds multiplied that by the height of the triangle which is still going to be four new thin meter just like. So calculating this, this will give us the a value or the total area under the curve to be seven new thin meter seconds or seven. And MS we wanna next scale our area under the curve with the moment of inertia. So scaling by I or the moment of inertia, we will then get the area under the curve to be seven Newton meter seconds divided by the moment of inertia. I which will equals to be seven Newton meter seconds divided by 3.5 kg meters squared. That will give us the total area under the curve to be two radiant per secondss. Awesome. So now that we get our area under the curve, we can substitute that back into our um kinematic rotational kinematic equation that we have here. And we can write that down which is omega F equals omega I plus A, our omega I is given to be 1.3 radiant per second. And the area under the curve is given to be two radiant for seconds. And that will give us the final angular velocity of 3.3 radiant per seconds. So with the final angular velocity of 3.3 radium per second option C is actually going to be the answer to this particular practice problem with the final angular velocity of the bar at P equals 2.5 seconds being 3.3 radiant for seconds. So that will be it for this particular video. If you guys still have any sort of confusion, please make sure to check out our other lesson videos on similar topics and that'll be it for this one. Thank you.