A 124 kg balloon carrying a 22 kg basket is descending with a constant downward velocity of 20.0 m/s. A 1.0 kg stone is thrown from the basket with an initial velocity of 15.0 m/s perpendicular to the path of the descending balloon, as measured relative to a person at rest in the basket. That person sees the stone hit the ground 5.00 s after it was thrown. Assume that the balloon continues its downward descent with the same constant speed of 20.0 m/s. How high is the balloon when the rock is thrown?

Question

Accepted Answer

Hey everyone, welcome back in this problem, We have 20 magic balls through each, a quarter of a kilogram, and they're in this thin bag and the bag has negligible weight, and the bag of magic balls is carried by a 90 kg flowing genie, and he's descending with a constant downward velocity of eight m per second. Okay, one of the magic balls gets thrown from the bag at six m per second, perpendicular, lee to the downward path of the genie. After 12 seconds, the Genie sees the Magic Ball bounce for the first time. Okay, and what we want to do is we want to calculate how far the Genie was from the ground when the Magic Ball was thrown. All right, now, we're going to assume that the Genie continues his descent at that same constant speed of 8m/s after the ball gets thrown. Okay, so we have our bag, let's just draw. What's going on here? We have our bag, Okay? And it has 20 magic balls. Alright? Each weigh a quarter of a kilogram so, altogether these balls weigh five kg with this genie kind of holding onto the bag here and then genie is descending with the bag eight m per second. Okay, And let's go ahead and say that down into the right is going to be our positive directions. Okay, So that we can say that that's a positive eight m per second. Alright, so the ball is going to get thrown from the bag. You can imagine the ball getting thrown and it's getting thrown with a speed of six m per second, perpendicular, okay, to the downward path, so straight out to the right, okay, and the ball is going to do something like this and it's gonna fall and it's gonna hit the ground. Okay? After 12 seconds. The Genie, after 12 seconds, the Genie sees the ball hit the ground for the first time, So T equals 12 seconds. It's hit the ground. All right. Now, when we're thinking about the motion of the ball, this distance here is gonna be delta Y. Okay, that's the distance that the ball travels, but it's also going to equal, we'll call it H. Okay, And that's gonna be the height of the genie when the ball was thrown, right? Because the genie we're assuming the ball and the genius at the same height when that ball is thrown. Okay. And so the distance that ball traveled is gonna be the same as the height of the genie when it was thrown. So this delta Y equals H is actually what we're looking for. Okay. All right, so, let's get started and when we're thinking about a problem like this, we want to think about, are you a. M. Equations? Okay, Our motion equations, let's think about the ball. And in this case we're looking for delta Y. So let's start with the Y. Direction. What do we know about the Y direction? Well, we know that be not Is going to be eight m/s. Okay, So even though that ball is being thrown out of the bag, it's initial downward velocity is going to be the same as the downward velocity of the bag. Okay? It's still moving with that same velocity that it was in the bag. So its initial downward velocity is going to be 8m/s. Okay. We don't know anything about its final velocity delta Y. We don't know but that's what we're looking for. Okay, So we want to find that delta Y. Okay. A well, we have the acceleration due to gravity because we've chosen down as a positive Y direction, this is going to be a positive 9.8 m per second squared. Okay. And finally, T. We know that T is 12 seconds. All right. So, we have three variables that we know the values of We have one that we're looking for so we can use our um equations. Okay. And the one that we're gonna chooses the one without VF. And that's gonna be delta Y. Is equal to v naught T plus one half a T squared, substituting the values, we know delta Y is equal to eight m per second times 12 seconds plus one half a which is 9.8 m per second squared times 12 seconds squared. Working this out the left term, we have meters per second time second. Okay, so the unit of second will cancel. We'll just be left with meters so we get 96 m. Okay? And similarly, in the second term, we have meters per second squared times seconds squared. So we're left with just meters. Okay? So we get 705.6 m there for a total delta Y of 801. m. Okay. And so again, this is Delta Y. This is the distance in the Y direction the ball traveled, which is the same as h the height of the genie when the ball was thrown. Okay? We went back up to our question. The answer is going to be 8 801.6 m. Thanks everyone for watching. See you in the next video.

Verified video answer for a similar problem:

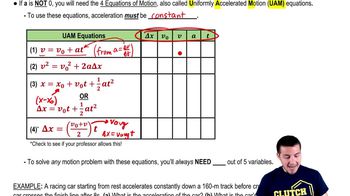
Key Concepts

Relative Velocity

Projectile Motion

Kinematic Equations