Home Repair. You need to extend a 2.50-inch-diameter pipe, but you have only a 1.00-inch-diameter pipe on hand. You make a fitting to connect these pipes end to end. If the water is flowing at 6.00 cm/s in the wide pipe, how fast will it be flowing through the narrow one?

At one point in a pipeline the water's speed is 3.00 m/s and the gauge pressure is 5.00×104 Pa. Find the gauge pressure at a second point in the line, 11.0 m lower than the first, if the pipe diameter at the second point is twice that at the first.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Bernoulli's Equation
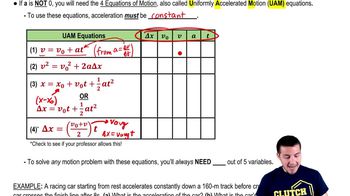
Continuity Equation

Hydrostatic Pressure

BIO. Artery Blockage. A medical technician is trying to determine what percentage of a patient's artery is blocked by plaque. To do this, she measures the blood pressure just before the region of blockage and finds that it is 1.20×104 Pa, while in the region of blockage it is 1.15×104 Pa. Furthermore, she knows that blood flowing through the normal artery just before the point of blockage is traveling at 30.0 cm/s, and the specific gravity of this patient's blood is 1.06. What percentage of the cross-sectional area of the patient's artery is blocked by the plaque?
A small circular hole 6.00 mm in diameter is cut in the side of a large water tank, 14.0 m below the water level in the tank. The top of the tank is open to the air. Find (a) the speed of efflux of the water and (b) the volume discharged per second.
A soft drink (mostly water) flows in a pipe at a beverage plant with a mass flow rate that would fill 220 0.355-L cans per minute. At point 2 in the pipe, the gauge pressure is 152 kPa and the cross-sectional area is 8.00 cm2. At point 1, 1.35 m above point 2, the cross-sectional area is 2.00 cm2. Find the (b) volume flow rate. (c) flow speeds at points 1 and 2.
A pressure difference of 6.00 × 104 Pa is required to maintain a volume flow rate of 0.800m3/s for a viscous fluid flowing through a section of cylindrical pipe that has radius 0.210 m. What pressure difference is required to maintain the same volume flow rate if the radius of the pipe is decreased to 0.0700 m?
