A very long insulating cylinder of charge of radius cm carries a uniform linear density of nC/m. If you put one probe of a voltmeter at the surface, how far from the surface must the other probe be placed so that the voltmeter reads V?

Two large, parallel conducting plates carrying opposite charges of equal magnitude are separated by cm. The surface charge density for each plate has magnitude nC/m^2. If the separation between the plates is doubled while the surface charge density is kept constant at the given value, what happens to the magnitude of the electric field and to the potential difference?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Electric Field Between Parallel Plates
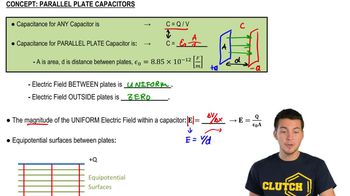
Potential Difference

Surface Charge Density

Two large, parallel conducting plates carrying opposite charges of equal magnitude are separated by cm. If the surface charge density for each plate has magnitude nC/m2, what is the magnitude of in the region between the plates?
Two large, parallel conducting plates carrying opposite charges of equal magnitude are separated by cm. What is the potential difference between the two plates?
Certain sharks can detect an electric field as weak as V/m. To grasp how weak this field is, if you wanted to produce it between two parallel metal plates by connecting an ordinary V AA battery across these plates, how far apart would the plates have to be?
How much excess charge must be placed on a copper sphere cm in diameter so that the potential of its center, relative to infinity, is kV? What is the potential of the sphere's surface relative to infinity?
A metal sphere with radius is supported on an insulating stand at the center of a hollow, metal, spherical shell with radius . There is charge on the inner sphere and charge on the outer spherical shell. Calculate the potential for (i) ; (ii) ; (iii) . (Hint: The net potential is the sum of the potentials due to the individual spheres.) Take to be zero when is infinite.
