A slit 0.240 mm wide is illuminated by parallel light rays of wavelength 540 nm. The diffraction pattern is observed on a screen that is 3.00 m from the slit. The intensity at the center of the central maximum (θ = 0°) is 6.00 x 10-6 W/m2. What is the distance on the screen from the center of the central maximum to the first minimum?

A single-slit diffraction pattern is formed by monochromatic electromagnetic radiation from a distant source passing through a slit 0.105 mm wide. At the point in the pattern 3.25° from the center of the central maximum, the total phase difference between wavelets from the top and bottom of the slit is 56.0 rad. What is the wavelength of the radiation?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Diffraction

Phase Difference
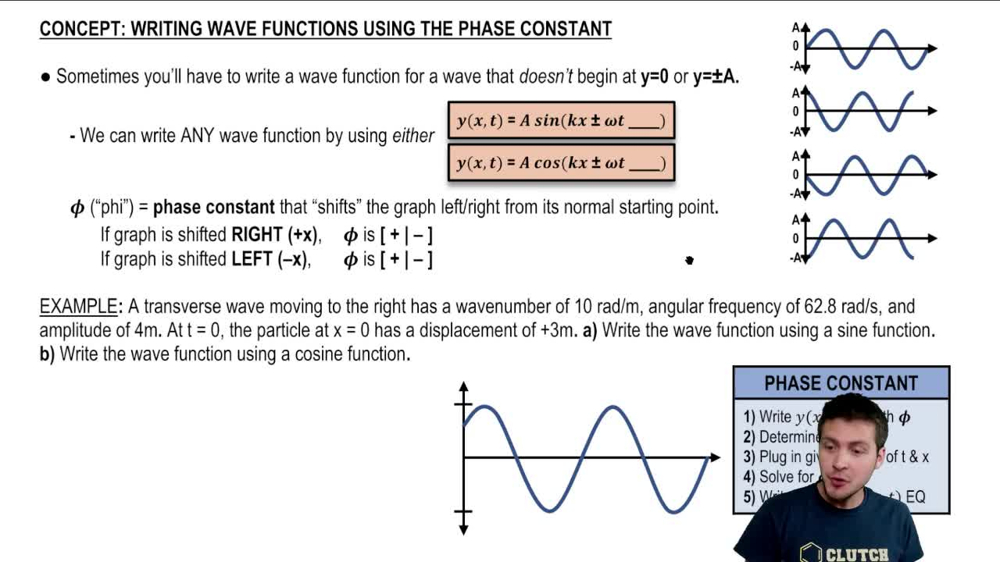
Wavelength

A slit 0.240 mm wide is illuminated by parallel light rays of wavelength 540 nm. The diffraction pattern is observed on a screen that is 3.00 m from the slit. The intensity at the center of the central maximum (θ = 0°) is 6.00 x 10-6 W/m2. What is the intensity at a point on the screen midway between the center of the central maximum and the first minimum?
Monochromatic light of wavelength 592 nm from a distant source passes through a slit that is 0.0290 mm wide. In the resulting diffraction pattern, the intensity at the center of the central maximum (θ = 0°) is 4.00x10-5 W/m2. What is the intensity at a point on the screen that corresponds to θ = 1.20°?
A single-slit diffraction pattern is formed by monochromatic electromagnetic radiation from a distant source passing through a slit 0.105 mm wide. At the point in the pattern 3.25° from the center of the central maximum, the total phase difference between wavelets from the top and bottom of the slit is 56.0 rad. What is the intensity at this point, if the intensity at the center of the central maximum is I0?
Parallel rays of monochromatic light with wavelength 568 nm illuminate two identical slits and produce an interference pattern on a screen that is 75.0 cm from the slits. The centers of the slits are 0.640 mm apart and the width of each slit is 0.434 mm. If the intensity at the center of the central maximum is 5.00 x 10-4 W/m2, what is the intensity at a point on the screen that is 0.900 mm from the center of the central maximum?
Laser light of wavelength 500.0 nm illuminates two identical slits, producing an interference pattern on a screen 90.0 cm from the slits. The bright bands are 1.00 cm apart, and the third bright bands on either side of the central maximum are missing in the pattern. Find the width and the separation of the two slits.
