Textbook Question
Write the expression for the ion product constant for water, Kw.
645
views

 Verified step by step guidance
Verified step by step guidance
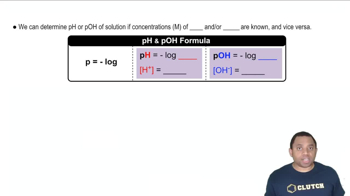


Write the expression for the ion product constant for water, Kw.
Calculate [H+] for each of the following solutions, and indicate whether the solution is acidic, basic, or neutral: (a) [OH-] = 0.00045 M (b) [OH-] = 8.8 × 10-9 M (c) a solution in which [OH-] is 100 times greater than [H+].
Calculate 3OH-4 for each of the following solutions, and indicate whether the solution is acidic, basic, or neutral: (a) 3H+4 = 0.0505 M
Calculate 3OH-4 for each of the following solutions, and indicate whether the solution is acidic, basic, or neutral: (c) a solution in which 3H+4 is 1000 times greater than 3OH-4.