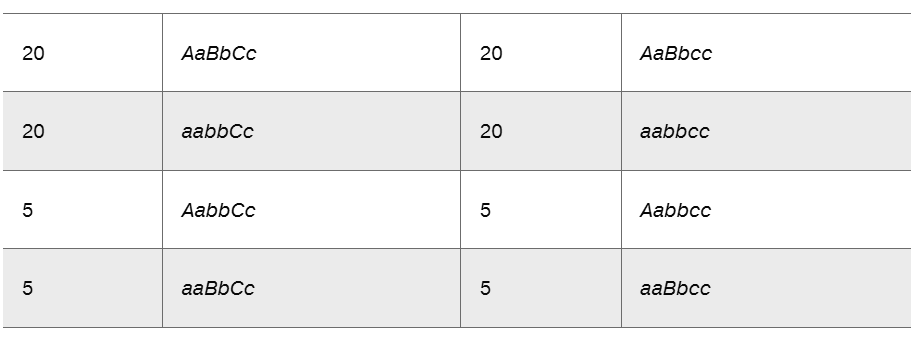
An organism of the genotype AaBbCc was testcrossed to a triply recessive organism (aabbcc). The genotypes of the progeny are presented in the following table. 20 AaBbCc 20 AaBbcc 20 aabbCc 20 aabbcc 5 AabbCc 5 Aabbcc 5 aaBbCc 5 aaBbcc If these three genes were all assorting independently, how many genotypic and phenotypic classes would result in the offspring, and in what proportion, assuming simple dominance and recessiveness in each gene pair?

Video transcript

Hello everyone and welcome to today's video. So we have a try hybrid cross that was done between a male with fully homosexuals, dominant genotype and a female that is fully homicide goes recessive phenotype. And the F. One progeny y self determine the fanatic, pick probability of the F two generation offspring having dominant phenotype for all three traits. The way that we're going to be doing this is that we're going to be using a couple of tracks that should make this process easier. So basically we're going to determine the genotype of the F. One generation. Using the following trick, we're going to select only one of the genotype. In this case we're going to select gene A and we're going to cross it. We're going to see that all the offspring are going to be heterosexuals for this gene. Now because all other genes are homosexuals, dominant and recessive they're going to be very similar. So in the end the resulting F1 generation is going to be fully hetero sagas for all genes because they follow the same inheritance method. No, now we have the F one generation and we're told that this F one generation was solved, meaning that it was crossed with an organism that has the same gina types. Now if we use the same trick because all of the genotype are the same in this case heterocyclic. We're going to see that we obtain probability. That is very interesting. So let's use a again. So we have one home a cycle is dominant to hetero zegas and one homicide was recessive. Were asked in the question to determine the fanatic probability of the F. Two generation having dominant phenotype in this case three out of four are going to have dominant phenotype which is going to be these three because they have at least one dominant. However, this is only determining the probability for A. Which is three out of four. We also have B. And we have C. So in in general which which is going to have to power this to the three or just multiply three divided by 43 times. And this is going to be equal to Divided by 64. And that is the probability of obtaining these dominant phenotype in the F- two generation. And that's going to be represented by answer choice. I really hope this helped you and I hope to see you on the next one.