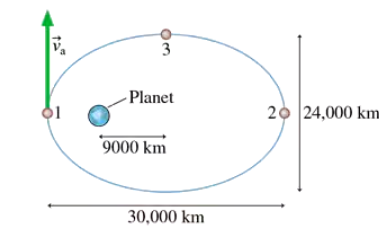
A satellite follows the elliptical orbit shown in FIGURE P12.77. The only force on the satellite is the gravitational attraction of the planet. The satellite's speed at point 1 is 8000 m/s. What is the satellite's speed at point 2?

Verified step by step guidance

1. Step 1: Recognize that the problem involves conservation of mechanical energy. Since the only force acting on the satellite is gravity, the total mechanical energy (kinetic + potential) of the satellite remains constant throughout its orbit.
2. Step 2: Write the expression for the total mechanical energy at point 1 and point 2. The total energy is given by: \( E = K + U \), where \( K \) is the kinetic energy \( \frac{1}{2}mv^2 \) and \( U \) is the gravitational potential energy \( -\frac{GMm}{r} \). Here, \( m \) is the satellite's mass, \( v \) is its speed, \( G \) is the gravitational constant, \( M \) is the planet's mass, and \( r \) is the distance from the center of the planet.
3. Step 3: Set the total energy at point 1 equal to the total energy at point 2: \( \frac{1}{2}mv_1^2 - \frac{GMm}{r_1} = \frac{1}{2}mv_2^2 - \frac{GMm}{r_2} \). Here, \( v_1 \) and \( r_1 \) are the speed and distance at point 1, and \( v_2 \) and \( r_2 \) are the speed and distance at point 2.
4. Step 4: Simplify the equation by canceling \( m \) (since it appears in every term) and solving for \( v_2 \): \( v_2 = \sqrt{v_1^2 + 2GM \left( \frac{1}{r_1} - \frac{1}{r_2} \right)} \). This equation relates the satellite's speed at point 2 to its speed at point 1 and the distances \( r_1 \) and \( r_2 \).
5. Step 5: Substitute the given values into the equation. Use \( v_1 = 8000 \, \text{m/s} \), \( r_1 \) (distance at point 1), and \( r_2 \) (distance at point 2) as provided in the problem or figure. Also, use the known values for \( G \) and \( M \) (gravitational constant and planet's mass). Perform the calculations to find \( v_2 \).

Key Concepts

Gravitational Force

Gravitational force is the attractive force between two masses, described by Newton's law of universal gravitation. It dictates that the force is proportional to the product of the masses and inversely proportional to the square of the distance between their centers. In the context of a satellite, this force is what keeps it in orbit around a planet.

Conservation of Energy

The principle of conservation of energy states that the total energy in a closed system remains constant. For a satellite in orbit, its mechanical energy, which is the sum of kinetic and potential energy, is conserved. As the satellite moves through different points in its elliptical orbit, its speed changes, but the total energy remains the same.

Elliptical Orbits

Elliptical orbits are paths followed by objects in space under the influence of gravity, characterized by their oval shape. According to Kepler's laws of planetary motion, a satellite moves faster when it is closer to the planet (periapsis) and slower when it is farther away (apoapsis). This variation in speed is crucial for calculating the satellite's speed at different points in its orbit.