Determine the moment of inertia about the axis of the object shown in FIGURE P12.52.

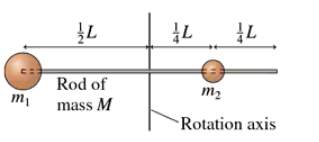
Verified step by step guidance

1. Step 1: Identify the axis of rotation specified in the problem and analyze the geometry of the object shown in FIGURE P12.52. Determine whether the object is composed of simple shapes (e.g., rods, disks, spheres) for which standard formulas for moment of inertia are available.
2. Step 2: Break the object into its constituent parts if it is a composite object. For each part, determine its mass, shape, and distance from the axis of rotation. Use the appropriate formula for the moment of inertia for each shape. For example, for a thin rod rotating about its center, the formula is \( I = \frac{1}{12} m L^2 \), and for a solid disk rotating about its center, the formula is \( I = \frac{1}{2} m R^2 \).
3. Step 3: If any part of the object is not rotating about its own center of mass, apply the parallel axis theorem to account for the offset. The parallel axis theorem states \( I = I_{\text{cm}} + m d^2 \), where \( I_{\text{cm}} \) is the moment of inertia about the center of mass, \( m \) is the mass, and \( d \) is the distance from the center of mass to the axis of rotation.
4. Step 4: Sum the moments of inertia of all the individual parts to find the total moment of inertia of the object about the specified axis. This is done using \( I_{\text{total}} = \sum I_{\text{individual}} \).
5. Step 5: Verify the units of the moment of inertia to ensure they are consistent (typically \( \text{kg} \cdot \text{m}^2 \)). Double-check the calculations and assumptions made for each part of the object to ensure accuracy.

Key Concepts

Moment of Inertia

The moment of inertia is a scalar value that quantifies an object's resistance to rotational motion about a specific axis. It depends on the mass distribution relative to that axis; the further the mass is from the axis, the greater the moment of inertia. It is calculated using the formula I = Σ(m_i * r_i^2), where m_i is the mass of each particle and r_i is the distance from the axis of rotation.

Axis of Rotation

The axis of rotation is an imaginary line around which an object rotates. The choice of this axis is crucial because the moment of inertia varies with different axes. For example, the moment of inertia about a central axis will differ from that about an edge, affecting the dynamics of the object's rotation.

Parallel Axis Theorem

The parallel axis theorem is a principle that allows the calculation of the moment of inertia of an object about any axis parallel to an axis through its center of mass. It states that I = I_cm + Md^2, where I_cm is the moment of inertia about the center of mass, M is the total mass, and d is the distance between the two axes. This theorem is particularly useful when dealing with composite objects or when the axis of interest is not through the center of mass.