Evaluate the cross products and A ✕ B and C ✕ D.

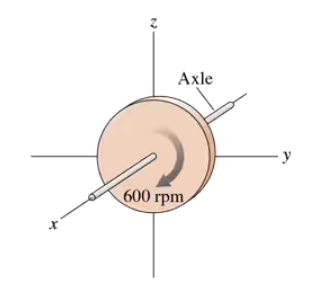
What is the angular momentum vector of the 2.0 kg, 4.0-cm-diameter rotating disk in FIGURE EX12.43? Give your answer using unit vectors.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Angular Momentum

Moment of Inertia

Unit Vectors

Vector A = 3î+ĵ and vector B= 3î - 2ĵ + 2k. What is the cross product A ✕ B?
Force is exerted on a particle at . What is the torque on the particle about the origin?
What is the angular momentum vector of the 500 g rotating bar in FIGURE EX12.44? Give your answer using unit vectors.
A 2.0 kg, 20-cm-diameter turntable rotates at 100 rpm on frictionless bearings. Two 500 g blocks fall from above, hit the turntable simultaneously at opposite ends of a diameter, and stick. What is the turntable's angular velocity, in rpm, just after this event?
A 75 g, 6.0-cm-diameter solid spherical top is spun at 1200 rpm on an axle that extends 1.0 cm past the edge of the sphere. The tip of the axle is placed on a support. What is the top's precession frequency in rpm?
