At what height above the earth is the free-fall acceleration 10% of its value at the surface?

Verified step by step guidance

1. Start by recalling the formula for gravitational acceleration: $g\; =\; Gm/(r^2)$, where $G$ is the gravitational constant, $m$ is the mass of the Earth, and $r$ is the distance from the center of the Earth.
2. Set the free-fall acceleration at the desired height to 10% of the surface acceleration: $g\_\{height\}\; =\; 0.1g\_\{surface\}$. Substitute $g\_\{surface\}\; =\; Gm/(R^2)$, where $R$ is the radius of the Earth.
3. Equate the two expressions for gravitational acceleration: $0.1(Gm/(R^2))\; =\; Gm/(r^2)$. Cancel out $Gm$ from both sides, leaving $0.1/(R^2)\; =\; 1/(r^2)$.
4. Rearrange the equation to solve for $r$: $r\; =\; R/sqrt(0.1)$. This gives the distance from the center of the Earth where the free-fall acceleration is 10% of its surface value.
5. Finally, calculate the height above the Earth's surface by subtracting the Earth's radius from $r$: $height\; =\; r\; -\; R$. This is the required height above the Earth's surface.

Key Concepts

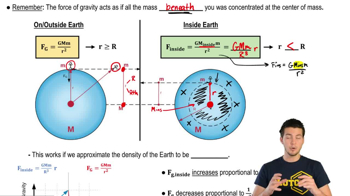
Free-Fall Acceleration

Free-fall acceleration, denoted as 'g', is the acceleration experienced by an object due solely to the force of gravity. At the Earth's surface, this value is approximately 9.81 m/s². As an object moves away from the Earth's surface, this acceleration decreases due to the inverse square law of gravitation.

Gravitational Force and Distance

The gravitational force between two masses decreases with the square of the distance between their centers. This relationship is described by Newton's law of universal gravitation, which states that the force is inversely proportional to the square of the distance. Therefore, as one moves further from the Earth, the gravitational pull diminishes, affecting the free-fall acceleration.

Height Above Earth's Surface

The height above the Earth's surface is a critical factor in determining the gravitational acceleration experienced by an object. To find the height at which the free-fall acceleration is 10% of its surface value, one must calculate the distance from the center of the Earth where this condition holds true, using the relationship between gravitational force and distance.