Water from a vertical pipe emerges as a 10-cm-diameter cylinder and falls straight down 7.5 m into a bucket. The water exits the pipe with a speed of 2.0 m/s. What is the diameter of the column of water as it hits the bucket?

Air flows through the tube shown in FIGURE P14.63. Assume that air is an ideal fluid. What is the volume flow rate?
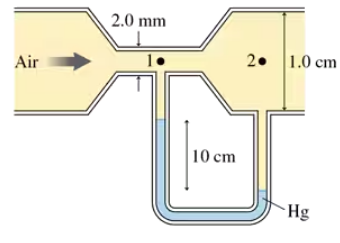
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Ideal Fluid

Bernoulli's Principle

Volume Flow Rate

A hurricane wind blows across a 6.0 m x 15.0 m flat roof at a speed of 130 km/h. What is the pressure difference?
Air flows through the tube shown in FIGURE P14.62 at a rate of 1200 cm³/s. Assume that air is an ideal fluid. What is the height h of mercury in the right side of the U-tube?
A water tank of height h has a small hole at height y. The water is replenished to keep h from changing. The water squirting from the hole has range 𝓍. The range approaches zero as y → 0 because the water squirts right onto the ground. The range also approaches zero as y → h because the horizontal velocity becomes zero. Thus there must be some height y between 0 and h for which the range is a maximum. Find an algebraic expression for the flow speed v with which the water exits the hole at height y.
A cylindrical tank of radius 𝑅, filled to the top with a liquid, has a small hole in the side, of radius 𝓇, at distance d below the surface. Find an expression for the volume flow rate through the hole.
20°C water flows through a 2.0-m-long, 6.0-mm-diameter pipe. What is the maximum flow rate in L/min for which the flow is laminar?
