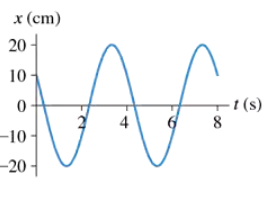
What are the (a) amplitude, (b) frequency, and (c) phase constant of the oscillation shown in FIGURE EX15.6?

Question

Accepted Answer

Welcome back, everyone. We are making observations about this periodic motion graph below and we are tasked with finding a couple different things here. In part one, we are going to find the maximum displacement. In part two, we are going to find the number of oscillations per second, otherwise known as the frequency. And in part three, we are going to find the phase constant of our periodic motion graph below. All right. So let's go ahead and start with part one here. But before doing that, let's read out our answer choices below. Answer choice A says for our maximum displacement is two centimeters, our frequency is 20.5 Hertz and our face constant is zero degrees. Answer choice B is four centimeters 40.25 Hertz and 60 degrees. Answer choice C is four centimeters four Hertz and 60 degrees. And answer choice D is eight centimeters 80.25 Hertz and negative degrees. All right. Moving on to part one here. What is going to be our maximum displacement here? Well, we're looking at our graph here's how you're able to tell the maximum displacement. What you want is you want the maximum amplitude or the peaks and valleys of our different curves here. And as you can see it goes between four and negative four. So the absolute value for our maximum displacement from zero centimeters is going to be four centimeters. All right. Move on to part two here. We need to figure out the frequency. Well, the frequency is just going to be given by one over the period of our periodic motion graph. Well, how do we calculate that? The way that we calculate that is we take from, we take the starting and end point of one entire cycle here. So let's start at two and then end at four. And you'll see that this, this path right here is one complete cycle as that will repeat over and over again, the distance of that is four seconds. So what we are going to do is we're gonna divide one by four and we get 40.25 Z wonderful. Now moving on to part three for our phase constant, we actually have a formula that we can use to find our phase constant. We have that the position at time T is equal to the amplitude times the cosine of omega T plus our phase constant. Well, let's go ahead and do or take the point T equal zero. So at T equals zero, we have that X is equal to two. So we have two is equal to our amplitude, which is just the answer to part one. So four times the cosine of zero plus our phase constant. What I'll do is I'll divide both sides by four and take the arc cosine or inverse cosine of each side. And what I get is that our phase constant is going to be equal to the inverse cosine of two divided by four which is just one half which gives us plus and minus 60 degrees. But which one is it, as you can see at time zero, we are in the positive X direction, not the negative X direct. Meaning that our face constant has the restriction that it must be between zero and 180 degrees and only one of our previous answers corresponds to that. So therefore, our face constant is equal to 60 degrees. So now we have found the maximum displacement, we have found the frequency and our face constant and all of these correspond to answer choice. B Thank you all so much for watching. I hope this video helped. We will see you all in the next one.

What are the (a) amplitude, (b) frequency, and (c) phase constant of the oscillation shown in FIGURE EX15.6?

Verified video answer for a similar problem:

Key Concepts

Amplitude

Frequency

Phase Constant