Integrated circuits are manufactured in vacuum chambers in which the air pressure is 1.0 x 10-10 of Hg. What are (a) the number density and (b) the mean free path of a molecule? Assume T = 20℃.

The molecules in a six-particle gas have velocities:
Calculate (a) , (b) , and (c) .
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Vector Addition

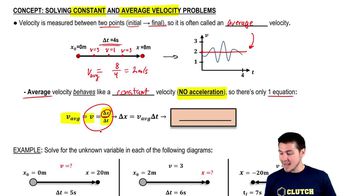
Average Velocity
Root Mean Square Velocity

A cylinder of nitrogen and a cylinder of neon are at the same temperature and pressure. The mean free path of a nitrogen molecule is 150 nm. What is the mean free path of a neon atom?
Eleven molecules have speeds 15, 16, 17, …, 25 m/s. Calculate (a) vavg and (b) vrms.
At 100℃ the rms speed of nitrogen molecules is 576 m/s. Nitrogen at 100℃ and a pressure of 2.0 atm is held in a container with a 10 cm x 10 cm square wall. Estimate the rate of molecular collisions (collisions/s) on this wall.
A cylinder contains gas at a pressure of 2.0 atm and a number density of 4.2 x 1025 m-3. The rms speed of the atoms is 660 m/s. Identify the gas.
The rms speed of molecules in a gas is 600 m/s. What will be the rms speed if the gas pressure and volume are both halved?
