A Carnot engine whose hot-reservoir temperature is 400℃ has a thermal efficiency of 40%. By how many degrees should the temperature of the cold reservoir be decreased to raise the engine's efficiency to 60%?

Verified step by step guidance

1. Step 1: Convert the temperatures of the hot reservoir from Celsius to Kelvin. The temperature in Kelvin is given by \( T(K) = T(°C) + 273.15 \). For the hot reservoir, \( T_h = 400 + 273.15 \).
2. Step 2: Recall the formula for the efficiency of a Carnot engine: \( \eta = 1 - \frac{T_c}{T_h} \), where \( \eta \) is the efficiency, \( T_c \) is the cold reservoir temperature in Kelvin, and \( T_h \) is the hot reservoir temperature in Kelvin.
3. Step 3: Use the given efficiency of 40% (or 0.40) to find the initial cold reservoir temperature \( T_c \). Rearrange the formula: \( T_c = T_h \cdot (1 - \eta) \). Substitute \( \eta = 0.40 \) and \( T_h \) from Step 1 to calculate \( T_c \).
4. Step 4: To achieve the new efficiency of 60% (or 0.60), use the same formula \( \eta = 1 - \frac{T_c}{T_h} \). Rearrange to find the new \( T_c \): \( T_c = T_h \cdot (1 - \eta) \). Substitute \( \eta = 0.60 \) and \( T_h \) from Step 1 to calculate the new \( T_c \).
5. Step 5: Determine the decrease in the cold reservoir temperature by subtracting the new \( T_c \) from the initial \( T_c \). Convert the result back to Celsius if needed by subtracting 273.15.

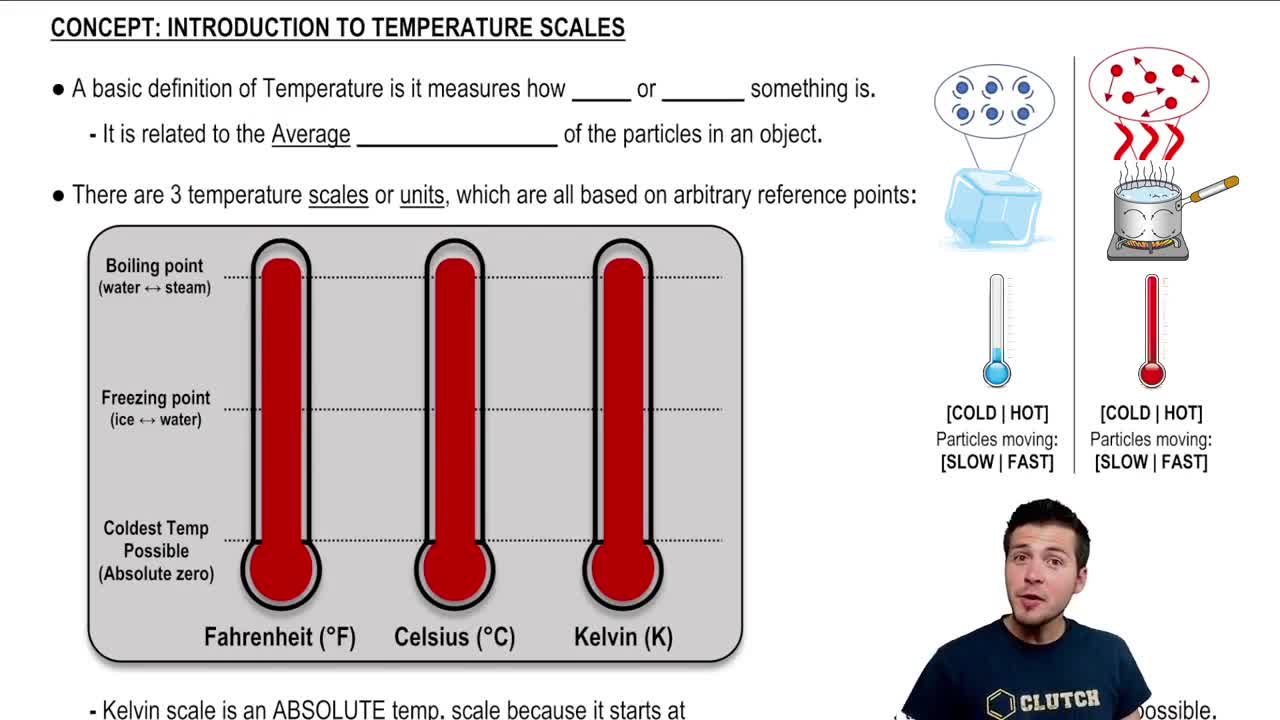
Key Concepts

Carnot Efficiency

Carnot efficiency is the maximum possible efficiency of a heat engine operating between two thermal reservoirs. It is defined by the formula η = 1 - (T_c / T_h), where η is the efficiency, T_c is the absolute temperature of the cold reservoir, and T_h is the absolute temperature of the hot reservoir. This concept highlights the relationship between temperature and efficiency, emphasizing that higher temperature differences can lead to greater efficiency.

Thermal Reservoirs

Thermal reservoirs are systems that can absorb or supply heat without undergoing a change in temperature. In the context of a Carnot engine, the hot reservoir provides heat to the engine, while the cold reservoir absorbs waste heat. The temperatures of these reservoirs are crucial in determining the engine's efficiency and performance, as they dictate the thermal gradient that drives the engine's operation.

Absolute Temperature Scale

The absolute temperature scale, measured in Kelvin (K), is a temperature scale that starts at absolute zero, the point where molecular motion ceases. To convert Celsius to Kelvin, one adds 273.15 to the Celsius temperature. This scale is essential in thermodynamics, particularly when calculating efficiencies and applying the Carnot theorem, as it ensures that temperature values are always positive and directly proportional to the thermal energy of the system.