A beam of unpolarized light of intensity I0 passes through a series of ideal polarizing filters with their polarizing axes turned to various angles as shown in Fig. E33.27. If we remove the middle filter, what will be the light intensity at point C?
Ch 33: The Nature and Propagation of Light

Young & Freedman Calc14th EditionUniversity PhysicsISBN: 9780321973610Not the one you use?Change textbook
All textbooks Young & Freedman Calc 14th Edition
Young & Freedman Calc 14th Edition Ch 33: The Nature and Propagation of Light
Ch 33: The Nature and Propagation of Light Problem 35a
Problem 35a
 Young & Freedman Calc 14th Edition
Young & Freedman Calc 14th Edition Ch 33: The Nature and Propagation of Light
Ch 33: The Nature and Propagation of Light Problem 35a
Problem 35aChapter 33, Problem 35a
A beam of white light passes through a uniform thickness of air. If the intensity of the scattered light in the middle of the green part of the visible spectrum is I, find the intensity (in terms of I) of scattered light in the middle of the red part of the spectrum.
 Verified step by step guidance
Verified step by step guidance1
Understand the concept of Rayleigh scattering, which explains how light is scattered by particles much smaller than the wavelength of light. The intensity of scattered light is inversely proportional to the fourth power of the wavelength: \( I \propto \frac{1}{\lambda^4} \).
Identify the wavelengths for the green and red parts of the visible spectrum. Green light typically has a wavelength around 550 nm, while red light is around 650 nm.
Express the intensity of scattered light for green light as \( I_g \) and for red light as \( I_r \). Since \( I_g \propto \frac{1}{\lambda_g^4} \) and \( I_r \propto \frac{1}{\lambda_r^4} \), we can relate \( I_r \) to \( I_g \) using the ratio of their wavelengths.
Set up the equation for the intensity ratio: \( \frac{I_r}{I_g} = \left( \frac{\lambda_g}{\lambda_r} \right)^4 \). Substitute the known wavelengths for green and red light into this equation.
Solve the equation to express \( I_r \) in terms of \( I_g \). This will give you the intensity of scattered light in the middle of the red part of the spectrum in terms of the intensity \( I \) of the green part.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
1mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rayleigh Scattering
Rayleigh scattering is the scattering of light or other electromagnetic radiation by particles much smaller than the wavelength of the light. It is responsible for the blue color of the sky and explains why shorter wavelengths (like blue and green) scatter more than longer wavelengths (like red). The intensity of scattered light is inversely proportional to the fourth power of the wavelength.
Recommended video:
Guided course

Law of Reflection
Visible Light Spectrum
The visible light spectrum is the portion of the electromagnetic spectrum that is visible to the human eye, ranging from approximately 380 nm to 750 nm. It includes colors from violet to red, with violet having the shortest wavelength and red the longest. Understanding the spectrum is crucial for analyzing how different wavelengths scatter differently.
Recommended video:
Guided course
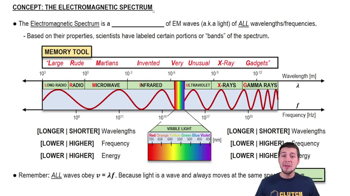
The Electromagnetic Spectrum
Intensity of Light
Intensity of light refers to the power per unit area carried by a wave. In the context of scattering, it is the amount of light energy scattered in a particular direction. The intensity of scattered light depends on factors like the wavelength of the light and the size of the scattering particles, as described by Rayleigh's law.
Recommended video:
Guided course

Wave Intensity
Related Practice
Textbook Question
1157
views
Textbook Question
Light of original intensity I0 passes through two ideal polarizing filters having their polarizing axes oriented as shown in Fig. E33.28. You want to adjust the angle f so that the intensity at point P is equal to I0/10. If the original light is unpolarized, what should Φ be?
895
views
Textbook Question
Light of original intensity I0 passes through two ideal polarizing filters having their polarizing axes oriented as shown in Fig. E33.28. You want to adjust the angle f so that the intensity at point P is equal to I0/10. If the original light is linearly polarized in the same direction as the polarizing axis of the first polarizer the light reaches, what should Φ be?
924
views