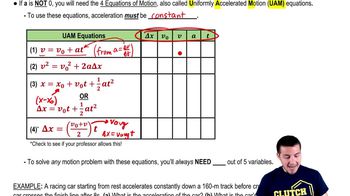
If a Tesla Model S P100D in 'Ludicrous mode' is pushed to its limit, the first of acceleration can be modeled as
What acceleration would be needed to achieve the same speed in the same time at constant acceleration? Give your answer as a multiple of .