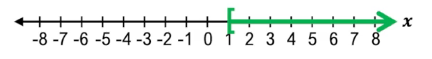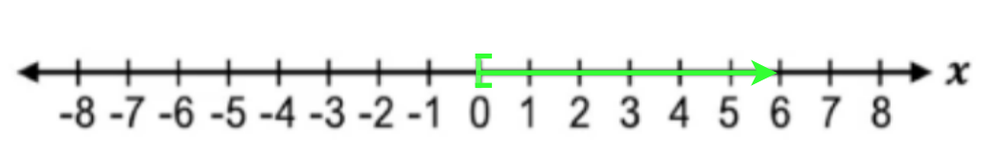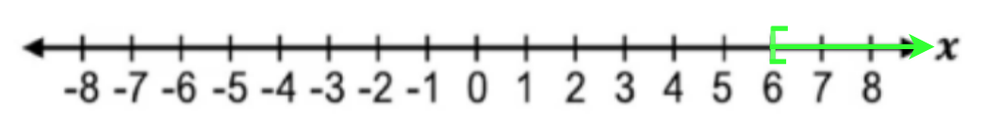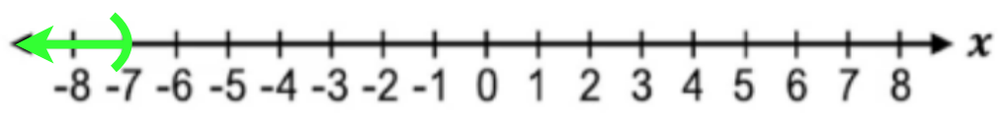Solving Linear Inequalities: Videos & Practice Problems

Linear inequalities, expressed as $\mathrm{ax}+b>c$ or with other inequality symbols, have solutions represented by ranges rather than single values. These solutions can be depicted using set builder notation, interval notation, or number lines with parentheses or brackets indicating inclusion or exclusion of boundary points. Solving inequalities involves isolating the variable using addition, subtraction, multiplication, or division, similar to linear equations. However, multiplying or dividing by a negative number requires flipping the inequality symbol to maintain a true statement, ensuring accurate solutions for inequalities.

Introduction to Linear Inequalities

Linear inequalities are closely related to linear equations but differ by using inequality symbols instead of an equal sign. While a linear equation typically takes the form \(ax + b = c\), a linear inequality replaces the equal sign with symbols such as \(>\), \(<\), \(\geq\), or \(\leq\), resulting in expressions like \(ax + b > c\). This subtle change transforms the problem from finding a single solution to identifying a range of solutions.

In a linear equation, solving for \(x\) yields a specific value that satisfies the equation. For example, solving \$2x - 6 = 0\( gives \)x = 3\(. However, when dealing with a linear inequality such as \)2x - 6 > 0\(, the solution is not a single number but all values of \)x\( that make the inequality true. In this case, solving the inequality results in \)x > 3\(, meaning any number greater than 3 satisfies the inequality.

To verify solutions of linear inequalities, you can substitute values from the solution range back into the inequality. For instance, plugging in \)x = 5\( into \)2x - 6 > 0\( yields \)2(5) - 6 = 10 - 6 = 4\(, and since \)4 > 0\( is true, \)x = 5\( is indeed a valid solution. This demonstrates that the solution to a linear inequality is a set of values rather than a single point.

Understanding linear inequalities involves recognizing their standard form \)ax + b \; \square \; c\(, where \)\square$ represents any inequality symbol. The solutions to these inequalities form intervals or ranges on the number line, contrasting with the single solutions typical of linear equations. This foundational knowledge sets the stage for exploring various methods to solve and graph linear inequalities, highlighting their similarities and differences with linear equations.

Representing Solutions to Linear Inequalities

When solving inequalities, the solution is not a single value but a range of values. Understanding how to represent and visualize these solution sets is essential. One common way to express inequalities is through set builder notation. For example, the inequality "x is greater than 3" can be written as the set of all x such that x > 3, denoted by \(\{ x \mid x > 3 \}\). The vertical bar means "such that," and the curly brackets enclose the entire solution set.

Another way to visualize inequalities is on a number line. To represent x > 3, you start at 3 and draw an arrow pointing to the right, indicating all values greater than 3. Since 3 itself is not included, this point is marked with a parenthesis or an open circle to show exclusion.

Interval notation provides a concise way to express these ranges. For x > 3, the interval is written as \((3, \infty)\), where the parenthesis around 3 indicates it is not included, and infinity always uses a parenthesis because it is not a finite value and cannot be included.

When the inequality includes the boundary value, such as x ≥ 3, the notations adjust accordingly. In set builder notation, it becomes \(\{ x \mid x \geq 3 \}\). On the number line, the point at 3 is included, represented by a closed circle or a square bracket. In interval notation, this is written as \([3, \infty)\), where the square bracket indicates inclusion of 3.

For inequalities where x is less than a value, such as x < 3, the same principles apply but the arrow on the number line points to the left. The set builder notation is \(\{ x \mid x < 3 \}\), and the interval notation is \((-\infty, 3)\) with parentheses indicating exclusion of both endpoints. If the inequality is x ≤ 3, then the set builder notation is \(\{ x \mid x \leq 3 \}\), the number line uses a closed circle or square bracket at 3, and the interval notation is \((-\infty, 3]\).

It is important to remember that infinity is never included in interval notation, so it is always enclosed in parentheses. Additionally, on number lines, open circles denote excluded values, while closed circles denote included values. Although parentheses and square brackets are more commonly used in graphs, recognizing open and closed circles is helpful for interpreting inequalities visually.

Mastering these notations—set builder, number line, and interval notation—enables clear communication and understanding of solution sets for linear inequalities, which is foundational for solving and graphing inequalities effectively.

Which inequality matches the graph?

• A. $x\ge 1$
• B. $x\le 1$
• C. $x>1$
• D.

Answer: (A)

Which inequality matches the graph?

• A. $x\ge1$
• B. $x\le1$
• C. $x>1$
• D. $x<1$

Answer: (D)

Use the number line to graph the following inequality.

$x\ge 6$

• A.
• B.
• C.
• D.

Answer: (C)

Use the number line to graph the following inequality.

$x\ge -7$

• A.
• B.
• C.
• D.

Answer: (A)

Write the following in interval notation.
$x\ge 0$

• A. $(-\infty ,0)$
• B. $[0,\infty )$
• C. $(0,\infty )$
• D. $(-\infty ,0]$

Answer: (B)

Write the following in interval notation.

• A. $(-\infty ,7]$
• B. $[7,\infty )$
• C. $(7,\infty )$
• D. $(-\infty ,7)$

Answer: (D)

Rewrite the following as an inequality statement.
$(-\infty ,2]$

• A. $x\le 2$
• B.
• C. $x\ge 2$
• D. $x>2$

Answer: (A)

Rewrite the following as an inequality statement.
$(1,\infty )$

• A. $x\ge 1$
• B. $x\le 1$
• C. $x>1$
• D. $$

Answer: (C)

Introduction to Linear Inequalities Example 1

Understanding how to translate between inequalities, interval notation, and graphical representations is essential for mastering the concept of inequalities. When given an inequality such as x > -2, it corresponds to the interval notation (-2, ∞), where the parenthesis indicates that -2 is not included in the set. This matches a graph starting just after -2 and extending infinitely to the right.

For inequalities that include the boundary value, such as x ≥ -5, the interval notation uses a square bracket to denote inclusion: [-5, ∞). This means the set includes -5 and all values greater than -5, which is reflected in the graph by a solid point at -5 and an arrow extending to infinity.

Intervals like (4, ∞) represent values greater than 4 but not including 4 itself, indicated by a parenthesis. The corresponding graph starts just after 4 and extends to the right, without including the point at 4.

When dealing with values less than a certain number, such as values less than -2, the interval notation is (-∞, -2), where the parenthesis again shows that -2 is not included. The graph for this interval starts from negative infinity and ends just before -2, with an open circle at -2.

Intervals that include the endpoint, like (-∞, 3], denote all values less than or equal to 3. The square bracket at 3 indicates inclusion, and the graph reflects this with a solid point at 3 and an arrow extending to the left towards negative infinity.

Finally, inequalities such as -1 ≤ x can be rewritten as x ≥ -1, showing that x is greater than or equal to -1. The interval notation is [-1, ∞), and the graph starts at -1 with a solid point and extends infinitely to the right.

By recognizing the symbols used in interval notation—parentheses ( ) for exclusion and brackets [ ] for inclusion—and understanding how these relate to inequalities and their graphical representations, one can confidently translate between these forms. This skill is fundamental in algebra and helps in solving and visualizing inequality problems effectively.

Solving Linear Inequalities

Solving linear inequalities involves isolating the variable using properties similar to those applied in linear equations, but with attention to the inequality symbols. The addition and subtraction properties of inequalities state that if A is greater than B, then adding or subtracting the same value C to both sides preserves the inequality:
\(A > B \implies A + C > B + C\) and \(A - C > B - C\).

For example, to solve \(x - 3 > 11\), add 3 to both sides to isolate x, resulting in \(x > 14\). This process mirrors solving linear equations but maintains the inequality symbol.

The multiplication and division properties of inequalities state that if A is greater than B, then multiplying or dividing both sides by a positive number C preserves the inequality:
\(A > B \implies A \times C > B \times C\) and \(A / C > B / C\) (for \(C > 0\)).

For instance, solving \$2 < \frac{x}{5}\( involves multiplying both sides by 5, yielding \)10 < x\(. The variable can be isolated on either side as long as the inequality remains true.

However, a critical difference arises when multiplying or dividing by a negative number. In such cases, the inequality symbol must be reversed to maintain a true statement. Formally, if A is greater than B and C is negative, then:
\)A > B \implies A \times C < B \times C\( and \)A / C < B / C\( (for \)C < 0\().

For example, solving \)-7x \geq 21\( requires dividing both sides by \)-7\(. Since \)-7\( is negative, the inequality flips, resulting in \)x \leq -3$. This flip accounts for the sign change caused by multiplication or division by a negative number, ensuring the solution remains valid.

In summary, solving linear inequalities involves isolating the variable using addition, subtraction, multiplication, and division properties similar to linear equations. The key distinction is that when multiplying or dividing by a negative number, the inequality symbol must be reversed to preserve the inequality's truth. Mastery of these principles allows for accurate solutions to linear inequalities across various contexts.

Solving Linear Inequalities Example 2

To solve the linear inequality x + 8 ≤ 12 - x, start by gathering all variable terms on one side and constants on the other. Add x to both sides to eliminate the negative x on the right, resulting in 2x + 8 ≤ 12. Next, subtract 8 from both sides to isolate the variable term: 2x ≤ 4. Finally, divide both sides by 2 to solve for x, giving x ≤ 2.

Graphing this solution on a number line involves marking the point at 2 and shading all values less than or equal to 2. Since the inequality includes equality (≤), use a closed circle or square bracket at 2 to indicate that 2 is part of the solution set.

Expressed in interval notation, the solution is (-∞, 2]. Here, the parenthesis around negative infinity indicates that it is not a specific number and cannot be included, while the square bracket at 2 shows that 2 is included in the interval.

This process demonstrates how to solve linear inequalities by applying inverse operations, similar to solving linear equations, while paying attention to inequality symbols to correctly represent the solution set both graphically and in interval notation.

Solve the following linear inequalities using the addition and subtraction properties of equality.
$5\le y+3$

• A. $2>y$
• B. $8\le y$
• C. $2\le y$
• D. $2\ge y$

Answer: (C)

Solve the following linear inequalities using the addition and subtraction properties of equality.
$x-2.3\le 4.1$

• A. $x\ge 6.4$
• B. $x>6.4$
• C. $x\le 6.4$
• D. $x\le 1.8$

Answer: (C)

Solve the following linear inequalities using the addition and subtraction properties of equality.

• A.
• B. $x>2$
• C.
• D. $x\le 1.8$

Answer: (A)

Solve the following linear inequalities and write the solution in interval notation.
$2(x+4)\le 3(x-1)+x$

• A. $\frac{11}{2}\ge x$
• B. $\frac{11}{2}\le x$
• C. $\frac{11}{4}\le x$
• D. $\frac{11}{4}\ge x$

Answer: (B)

Solve the following linear inequalities and write the solution in interval notation.

• A.
• B.
• C. $x>-\frac{18}{5}$
• D. $x>-\frac{5}{2}$

Answer: (C)

Solving Linear Inequalities Example 3

When solving inequalities, it is important to isolate the variable terms on one side and the constants on the other. Consider the inequality \$2x - 5 < 2x + 10\(. By subtracting \)2x\( from both sides, the variable terms cancel out, leaving \)-5 < 10\(. Since this statement is always true, the inequality holds for all real numbers. This means the solution set includes every real number because no matter what value of \)x\( is substituted, the inequality remains valid.

In contrast, examine the inequality \)x + 2 \geq x + 8\(. Subtracting \)x\( from both sides eliminates the variable terms, resulting in \)2 \geq 8\(. This is a false statement, indicating that the inequality has no solution. Such inequalities are called inconsistent because no value of \)x$ can satisfy them.

These examples illustrate key concepts in solving linear inequalities, similar to solving linear equations. An inequality can be an identity, true for all values of the variable, or inconsistent, with no possible solutions. Understanding these outcomes helps in analyzing and interpreting inequalities effectively.

Here’s what students ask on this topic:

What is a linear inequality and how does it differ from a linear equation?

A linear inequality is similar to a linear equation but instead of an equal sign, it uses inequality symbols such as >, <, ≥, or ≤. For example, a linear equation looks like $\mathrm{2x}-6=0$, while a linear inequality might be $\mathrm{2x}-6>0$. The key difference is that the solution to a linear equation is a single value of $x$ that makes the equation true, whereas the solution to a linear inequality is a range of values that satisfy the inequality. This means instead of one point, the solution is an interval or set of values on the number line.

How do you represent the solution of a linear inequality using interval notation?

Interval notation is a concise way to represent the solution set of a linear inequality. For example, if the solution is $x>3$, the interval notation is $(3,\infty )$. Parentheses indicate that the endpoint is not included. If the inequality is $x\ge 3$, then the interval notation is $[3,\infty )$, where the square bracket means the endpoint 3 is included. Infinity always uses parentheses because it is not a finite number and cannot be included. This notation helps visualize the range of values that satisfy the inequality.

What is the rule for solving linear inequalities when multiplying or dividing by a negative number?

When solving linear inequalities, if you multiply or divide both sides of the inequality by a negative number, you must reverse the direction of the inequality symbol. For example, if you have $-7x\ge 21$ and divide both sides by $-7$, the inequality flips from ≥ to ≤, resulting in $x\le -3$. This rule is essential because multiplying or dividing by a negative changes the order of the values, so flipping the inequality maintains a true statement. Forgetting to flip the inequality leads to incorrect solutions.

How can you graphically represent the solution of a linear inequality on a number line?

To graph the solution of a linear inequality on a number line, first identify the boundary point. For example, for $x>3$, place an open circle at 3 to show that 3 is not included. Then draw an arrow to the right indicating all values greater than 3 are included. If the inequality is $x\ge 3$, use a closed circle or square bracket at 3 to indicate inclusion, and draw the arrow to the right. For less than inequalities, the arrow points to the left. This visual helps understand the range of solutions clearly.

What are the different notations used to express the solution set of linear inequalities?

There are three common notations to express solutions of linear inequalities: set builder notation, interval notation, and number line graphs. Set builder notation uses curly braces and a vertical bar, for example, $\left\{x\right|x>3\}$, read as "the set of x such that x is greater than 3." Interval notation uses parentheses and brackets to show ranges, like $(3,\infty )$ for x > 3. Number line graphs visually represent the solution with open or closed circles and arrows indicating the direction of the inequality. Each notation provides a different way to understand and communicate the solution set.