Introduction to Relations and Functions: Videos & Practice Problems

Relations connect inputs (x values) to outputs (y values) and can be represented as ordered pairs, tables, graphs, or equations. A function is a special relation where each input corresponds to exactly one output. The vertical line test helps identify functions on graphs: if any vertical line crosses more than one point, it's not a function. The domain is the set of all input values, and the range is the set of all output values. For continuous graphs, domain and range are expressed using interval notation, capturing all possible x and y values within specified bounds.

Intro to Relations and Functions

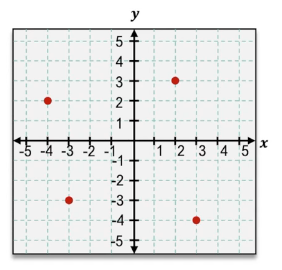
A relation is a connection between inputs (x-values) and outputs (y-values), often represented as a set of ordered pairs in the form \((x, y)\). To understand relations, you can list all the input values and output values separately and then show how each input corresponds to an output. For example, given ordered pairs like \((-2, 2)\), \((1, 1)\), \((3, -2)\), and \((1, 4)\), the inputs are \(-2\), \$1\(, and \)3\(, while the outputs are \)2\(, \)1\(, \)-2\(, and \)4\(. Notice that the input \)1\( corresponds to two different outputs, \)1\( and \)4\(.

A function is a special type of relation where each input is paired with at most one output. This means no input value maps to more than one output value. For instance, if you have ordered pairs like \)(-4, 2)\(, \)(-2, -1)\(, \)(1, 2)\(, and \)(3, 4)\(, each input corresponds to exactly one output. Here, \)-4\( maps to \)2\(, \)-2\( maps to \)-1\(, \)1\( maps to \)2\(, and \)3\( maps to \)4\(. Since no input repeats with different outputs, this relation qualifies as a function.

It is important to recognize that all functions are relations, but not all relations are functions. This distinction hinges on whether each input has a unique output.

Relations and functions can be represented in various ways beyond ordered pairs. They can be shown as correspondences, tables, graphs, or equations. For example, a function can be expressed as an equation like \)y = 2x + 3\(, which defines a unique output \)y\( for each input \)x$.

Understanding the difference between relations and functions is fundamental in mathematics, as it helps in analyzing how variables depend on each other and in identifying valid functions for modeling real-world scenarios.

Intro to Relations and Functions Example 1

To determine whether a relation is a function, it is essential to analyze the mapping between inputs (often represented as x-values) and outputs (y-values). A function is defined as a relation where each input corresponds to exactly one output. This means no single input can map to multiple outputs.

For example, consider a relation given in a table format. Begin by listing the unique input values. Then, observe the outputs associated with each input. If any input value is paired with more than one output value, the relation is not a function. For instance, if the input ½ maps to both 4 and 5, this violates the definition of a function because one input has multiple outputs.

Alternatively, when given a mapping diagram with inputs and outputs represented by letters or symbols, the exact numerical values of outputs are not necessary to determine if the relation is a function. The key is to verify that each input connects to only one output. If every input has a single corresponding output, the relation qualifies as a function.

In summary, the fundamental criterion for a function is that each input value must have at most one output value. This concept is crucial in understanding functions in algebra and helps distinguish functions from general relations.

Vertical Line Test

A function is a special type of relation where each input corresponds to exactly one unique output. To quickly determine whether a relation represented on a graph is a function, the vertical line test is an effective method. This test involves imagining or drawing vertical lines across the graph. If any vertical line intersects the graph at more than one point, the relation is not a function. Conversely, if every vertical line touches the graph at most once, the relation qualifies as a function.

When applying the vertical line test, consider a graph with discrete points. By drawing vertical lines through each point, if no line crosses more than one point, the graph represents a function. For example, a set of plotted points where each vertical line intersects only one point confirms the relation is a function.

In contrast, for graphs depicting smooth curves with infinitely many points, the vertical line test remains applicable. If any vertical line intersects the curve at multiple points, this indicates that a single input corresponds to multiple outputs, violating the definition of a function. For instance, a vertical line crossing a curve at two points shows the relation is not a function.

Understanding the vertical line test is essential for analyzing functions graphically. It provides a quick and reliable way to verify whether a relation meets the criteria of a function by ensuring each input has a unique output. This concept is fundamental in mathematics, especially when studying functions and their properties.

State the inputs and outputs of the following relation. Is it a function?
$\{(-3,5),(0,2),(3,5)\}$

• A.
• B.
• C.
• D.

Answer: (C)

State the inputs and outputs of the following relation. Is it a function?
$\{(2,5),(0,2),(2,9)\}$

• A.
• B.
• C.
• D.

Answer: (B)

Vertical Line Test Example 2

To determine whether a graph represents a function, the vertical line test is a useful method. This test states that if a vertical line can be drawn anywhere on the graph and it intersects the graph at more than one point, then the graph is not a function. Conversely, if every vertical line drawn intersects the graph at most once, then the graph is indeed a function.

For example, consider three different graphs:

1. **Graph A**: When applying the vertical line test, any vertical line drawn across this graph intersects it at only one point. This consistent behavior confirms that Graph A is a function.

2. **Graph B**: In this case, a vertical line can be drawn that intersects the graph at multiple points. This indicates that Graph B does not satisfy the criteria for a function.

3. **Graph C**: Similar to Graph A, any vertical line drawn on Graph C intersects it at only one point. Thus, Graph C is also classified as a function.

In summary, Graphs A and C are functions, while Graph B is not. This understanding of the vertical line test is essential for identifying functions in various mathematical contexts.

Domain and Range

Understanding the domain and range is essential when working with relations and functions. The domain refers to the set of all possible input values, typically represented as the x-values, while the range consists of all possible output values, or the y-values. These concepts help describe the behavior and limitations of functions and relations.

When given a relation as a set of ordered pairs or a table, finding the domain and range involves listing all the unique x-values for the domain and all the unique y-values for the range. For example, if a relation includes the ordered pairs (-2, 2), (1, 1), (3, -2), and (4, 4), the domain is the set {-2, 1, 3, 4} and the range is {2, 1, -2, 4}. This straightforward approach works well for discrete data points.

However, when dealing with continuous functions represented by graphs, the domain and range often include infinitely many values. In such cases, interval notation is used to express the domain and range efficiently. Interval notation uses brackets [ ] to indicate inclusion of endpoints and parentheses ( ) to indicate exclusion. For example, if a graph starts at x = -4 (included) and extends indefinitely to the right, the domain is written as \([-4, \infty)\). Similarly, if the range starts at y = -2 (included) and extends upward indefinitely, the range is \([-2, \infty)\).

Recognizing whether to list values explicitly or use interval notation depends on the nature of the relation or function. Discrete sets of points call for listing individual values, while continuous graphs require intervals to capture all possible inputs and outputs. Mastering domain and range allows for better analysis and understanding of functions, enabling you to predict their behavior and solve related problems effectively.

Find the domain and range for each relation.
(A) $\{(-4,2),(-3,-5),(3,4),(5,-2)\}$

• A. Domain: $\left\lbrace-4,-3,3,5\right\rbrace$, Range: $\left\lbrace-4,-3,2,5\right\rbrace$
• B. Domain: $\left\lbrace-4,-3,3,5\right\rbrace$, Range: $\left\lbrace2,-5,4,-2\right\rbrace$
• C. Domain: ,$\left\lbrace-4,2,3,5\right\rbrace$ Range: $\left\lbrace2,-5,4,-2\right\rbrace$
• D. Domain: $\left\lbrace-4,-3,3,5\right\rbrace$, Range: $\left\lbrace5,-2,4,-5\right\rbrace$

Answer: (B)

Find the domain and range for each relation.
(B)

• A. Domain: $\left\lbrace-4,2,3\right\rbrace$, Range: $\left\lbrace2,3,-4\right\rbrace$
• B. Domain: $\left\lbrace-4,-3,2,3\right\rbrace$, Range: $\left\lbrace1,2,-3,3,-4\right\rbrace$$\left\lbrace2,-3,3,-4\right\rbrace$
• C. Domain: $\left\lbrace-4,-3,3\right\rbrace$, Range: $\left\lbrace2,-3,3,-4\right\rbrace$
• D. Domain: $\left\lbrace-4,-3,2,3\right\rbrace$, Range: $\left\lbrace2,-3,3,-4\right\rbrace$

Answer: (D)

Domain and Range Example 3

To determine the domain and range of a function from its graph, it is essential to understand that the domain represents all possible x-values for which the function is defined, while the range includes all possible y-values that the function attains. Expressing these sets in interval notation provides a clear and concise way to describe them.

For example, consider a graph where the function exists starting just to the right of x = -4 and continues up to x = 2. If the graph has an open circle at x = -4, this indicates that the function does not include the value at x = -4, so the interval starts just after this point, denoted by a parenthesis. Conversely, if there is a closed circle at x = 2, the function includes this endpoint, represented by a bracket. Thus, the domain in this case is \((-4, 2]\).

Examining the range involves looking at the vertical extent of the graph. Suppose the function's lowest y-value is just above y = -4 (indicated by an open circle, so not included) and it reaches up to y = 5 with a closed circle (included). The range would then be \((-4, 5]\).

In contrast, if a graph extends infinitely in all directions, such as continuing without bound to the left and right and also infinitely upward and downward, the domain and range encompass all real numbers. This is expressed as \((-\infty, \infty)\) for both domain and range, indicating no restrictions on the values of x or y.

Understanding how to interpret open and closed circles on a graph is crucial for accurately writing domain and range in interval notation. Open circles mean the endpoint is excluded, while closed circles mean it is included. Recognizing whether the graph extends infinitely or is bounded helps determine if the intervals are finite or infinite. This approach allows for precise identification of the function's domain and range directly from its graphical representation.

Here’s what students ask on this topic:

What is the difference between a relation and a function in algebra?

A relation in algebra is a set of ordered pairs that connects inputs (x-values) to outputs (y-values). It can be represented as ordered pairs, tables, graphs, or equations. A function is a special type of relation where each input corresponds to exactly one output. This means that in a function, no input value is paired with more than one output value. For example, if an input x = 1 maps to y = 2 and also y = 4, then it is a relation but not a function. However, if each input maps to only one output, it is a function. All functions are relations, but not all relations are functions.

How do you use the vertical line test to determine if a graph represents a function?

The vertical line test is a quick way to determine if a graph represents a function. To use it, imagine drawing vertical lines through the graph at various points. If any vertical line crosses the graph at more than one point, then the graph does not represent a function. This is because multiple outputs exist for a single input, violating the definition of a function. If every vertical line crosses the graph at most once, then the graph represents a function. This test only applies when the relation is shown as a graph.

What are domain and range in the context of relations and functions?

The domain of a relation or function is the set of all possible input values (x-values), while the range is the set of all possible output values (y-values). For example, if you have a set of ordered pairs, the domain is the collection of all x-values, and the range is the collection of all y-values. When dealing with continuous graphs, the domain and range are often expressed using interval notation to represent all values within a certain span. For instance, if the graph covers x-values from -4 to infinity, the domain is written as $[-4,\infty )$. Similarly, the range is expressed based on the y-values covered.

How can relations be represented besides ordered pairs?

Relations can be represented in several ways besides ordered pairs. These include tables, where inputs and outputs are listed in rows; graphs, where points or curves show the relationship between x and y values; equations, which express the relation algebraically; and correspondences, which visually connect inputs to outputs using arrows. Each representation helps visualize or analyze the relation differently, and functions can also be represented using these methods if they meet the criteria of having one output per input.

Why is interval notation used for domain and range in continuous functions?

Interval notation is used for domain and range in continuous functions because these functions have infinitely many points within a range of values. Listing all individual x or y values is impossible, so interval notation efficiently describes the set of all input or output values. For example, if a function's graph starts at x = -4 and extends indefinitely to the right, the domain is written as $[-4,\infty )$. Brackets indicate that the endpoint is included, while parentheses indicate that infinity is not included. This notation clearly communicates the continuous span of values covered by the function.