One of the emission lines of the hydrogen atom has a wavelength of 94.974 nm. (b) Determine the initial and final values of n associated with this emission.
Ch.6 - Electronic Structure of Atoms

Brown14th EditionChemistry: The Central ScienceISBN: 9780134414232Not the one you use?Change textbook
Chapter 6, Problem 45
Order the following transitions in the hydrogen atom from smallest to largest frequency of light absorbed: n = 3 to n = 7, n = 4 to n = 8, n = 2 to n = 5, and n = 1 to n = 3.
 Verified step by step guidance
Verified step by step guidance1
Identify the initial and final energy levels for each transition. For example, for the transition n = 3 to n = 7, the initial level (ni) is 3 and the final level (nf) is 7.
Use the formula for the frequency of light absorbed during a transition in a hydrogen atom, which is derived from the energy difference between the two levels: \( \Delta E = E_f - E_i \) where \( E_n = -\frac{13.6 \text{ eV}}{n^2} \) for a hydrogen atom.
Calculate the energy difference for each transition using the formula: \( \Delta E = -13.6 \text{ eV} \left( \frac{1}{n_f^2} - \frac{1}{n_i^2} \right) \).
Convert the energy difference to frequency using the relation \( \Delta E = h \nu \), where \( h \) is Planck's constant. Solve for \( \nu \) to find the frequency: \( \nu = \frac{\Delta E}{h} \).
Compare the frequencies calculated for each transition to determine the order from smallest to largest frequency.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Energy Levels in Hydrogen Atom
In a hydrogen atom, electrons occupy discrete energy levels, denoted by quantum numbers (n). The energy associated with each level increases with n, meaning that transitions between levels involve the absorption or emission of energy in the form of light. The difference in energy between two levels determines the frequency of the light absorbed or emitted during a transition.
Recommended video:
Guided course

Hydrogenation Reactions
Rydberg Formula
The Rydberg formula provides a way to calculate the wavelengths (and thus frequencies) of light emitted or absorbed during electron transitions in hydrogen. It states that the frequency of light (ν) is proportional to the difference in the inverse squares of the principal quantum numbers (n) of the initial and final states. This relationship allows for the determination of the frequency based on the specific transitions being analyzed.
Recommended video:
Guided course
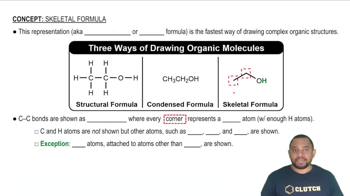
Skeletal Formula
Frequency and Energy Relationship
The frequency of light is directly related to its energy through the equation E = hν, where E is energy, h is Planck's constant, and ν is frequency. Higher energy transitions correspond to higher frequencies of light. Therefore, by calculating the energy differences for each transition, one can rank them from smallest to largest frequency absorbed.
Recommended video:
Guided course

Frequency-Wavelength Relationship
Related Practice
Textbook Question
1896
views
1
comments
Textbook Question
The hydrogen atom can absorb light of wavelength 1094 nm. (a) In what region of the electromagnetic spectrum is this absorption found?
Textbook Question
The hydrogen atom can absorb light of wavelength 1094 nm. (b) Determine the final value of n associated with this absorption.
1806
views
Textbook Question
Write the electron configurations for the following ions, anddetermine which have noble-gas configurations:(a) Ti2+(b) Br-(c) Mg2+(d) Po2-(e) Pt2+(f) V3+
1433
views
Textbook Question
Use the de Broglie relationship to determine the wavelengths of the following objects: (a) an 85-kg person skiing at 50 km/hr (b) a 10.0-g bullet fired at 250 m/s
695
views
Textbook Question
Use the de Broglie relationship to determine the wavelengths of the following objects: (c) a lithium atom moving at 2.5 × 105 m/s (d) an ozone (O3) molecule in the upper atmosphere moving at 550 m/s.
542
views
