Evaluate each expression without using a calculator.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
6. Exponential & Logarithmic Functions
Introduction to Logarithms
Problem 50
Textbook Question
Graph each function. ƒ(x) = log10 x
 Verified step by step guidance
Verified step by step guidance1
Understand that the function given is \( f(x) = \log_{10} x \), which is a logarithmic function with base 10. This means it is the inverse of the exponential function \( 10^x \).
Identify the domain of the function. Since logarithms are only defined for positive real numbers, the domain is \( x > 0 \). This means the graph will only exist to the right of the y-axis.
Plot key points by choosing values of \( x \) that are powers of 10, because \( \log_{10} 10^k = k \). For example, plot points at \( (1,0) \), \( (10,1) \), and \( (0.1, -1) \).
Draw the vertical asymptote at \( x = 0 \) because the logarithmic function approaches negative infinity as \( x \) approaches zero from the right.
Sketch the curve passing through the plotted points, increasing slowly and continuously for \( x > 0 \), reflecting the logarithmic growth behavior.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Logarithmic Functions
A logarithmic function is the inverse of an exponential function. For ƒ(x) = log₁₀(x), it answers the question: 'To what power must 10 be raised to get x?' Understanding this helps in interpreting the behavior and values of the function.
Recommended video:
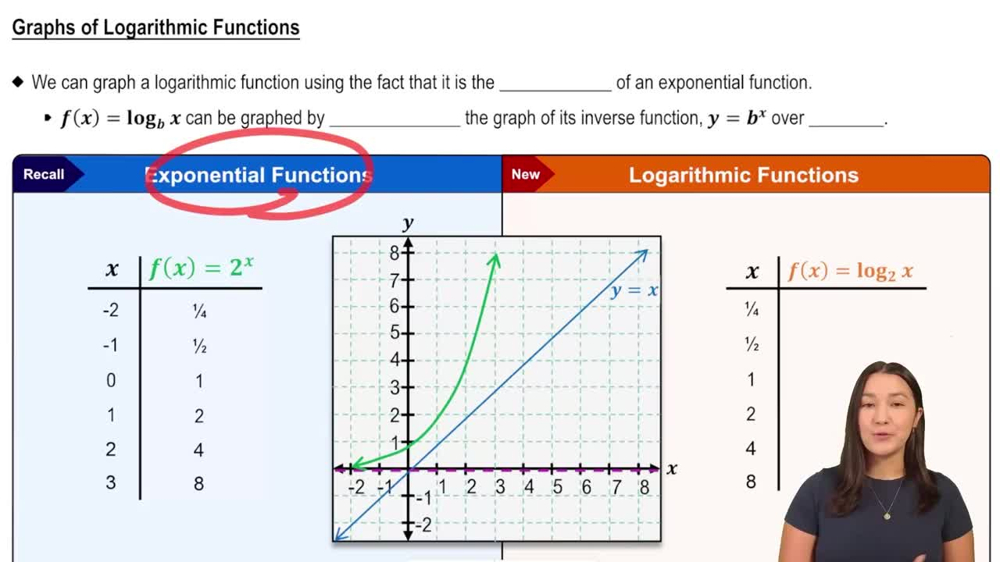
Graphs of Logarithmic Functions
Domain of Logarithmic Functions
The domain of ƒ(x) = log₁₀(x) includes all positive real numbers (x > 0) because logarithms of zero or negative numbers are undefined in the real number system. Recognizing the domain is essential for correctly graphing the function.
Recommended video:

Graphs of Logarithmic Functions
Graphing Logarithmic Functions
Graphing involves plotting points that satisfy the function and understanding key features like the vertical asymptote at x = 0, the x-intercept at (1,0), and the increasing nature of the graph. This helps visualize how the function behaves across its domain.
Recommended video:

Graphs of Logarithmic Functions
Related Videos
Related Practice
Textbook Question
664
views


