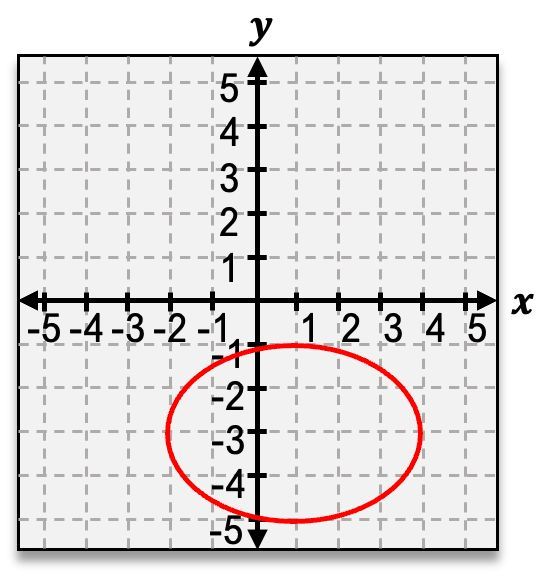
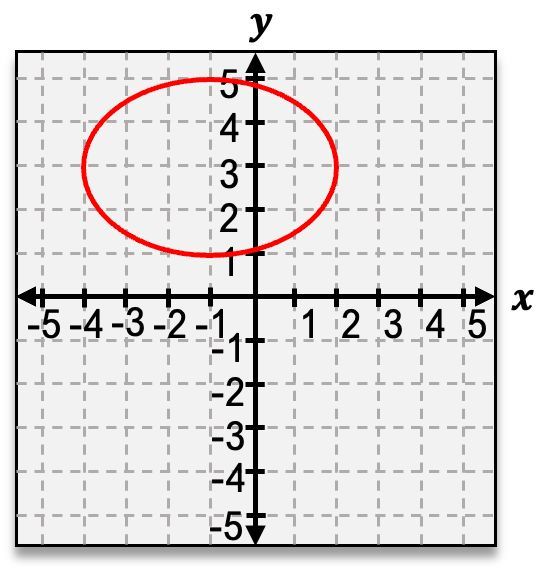
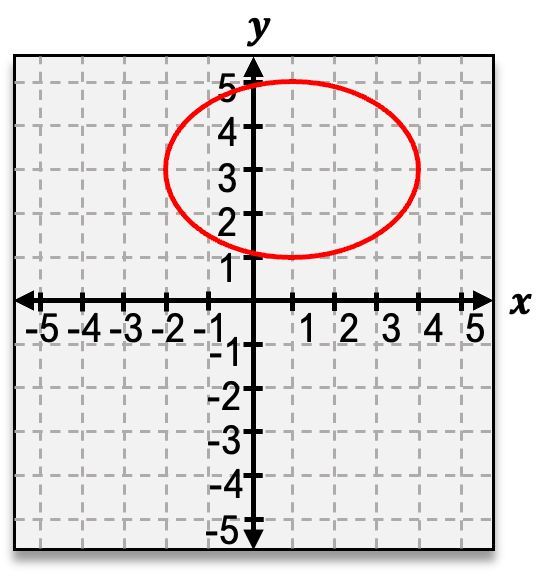
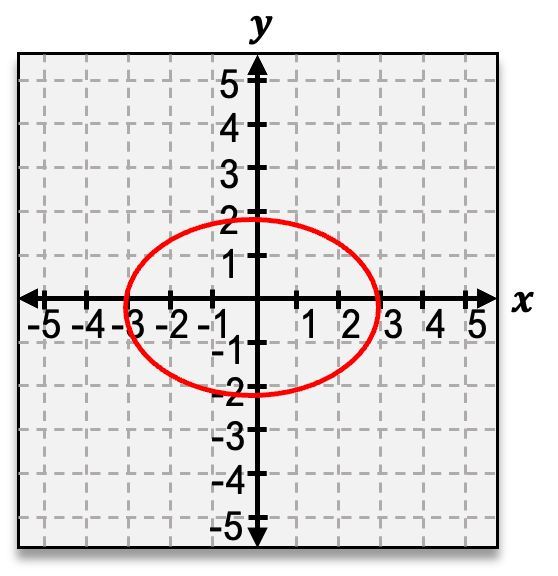
In the study of conic sections, the ellipse is a fascinating shape that emerges when a three-dimensional cone is intersected by a two-dimensional plane at a slight angle. Unlike the circle, which is defined by a single radius, the ellipse requires the consideration of two distinct distances: the semi-major axis and the semi-minor axis. The semi-major axis, denoted as \( a \), represents the longest distance from the center of the ellipse to its edge, while the semi-minor axis, denoted as \( b \), is the shorter distance.
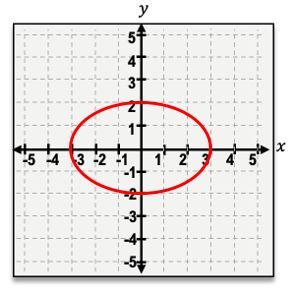
When visualizing a horizontal ellipse, the semi-major axis extends along the x-axis, and the semi-minor axis extends along the y-axis. The equation for a horizontal ellipse can be expressed as:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
For example, if \( a = 4 \) and \( b = 3 \), the equation becomes:
\[ \frac{x^2}{16} + \frac{y^2}{9} = 1 \]
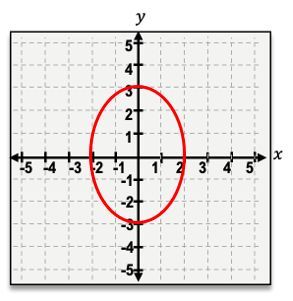
Conversely, when the ellipse is vertically stretched, the semi-major axis aligns with the y-axis, and the semi-minor axis aligns with the x-axis. The equation for a vertical ellipse is structured as follows:
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \]
Using the same values, the equation for a vertical ellipse would be:
\[ \frac{x^2}{9} + \frac{y^2}{16} = 1 \]
It is essential to recognize that the variable \( a \) consistently indicates the longest distance from the center to the ellipse's edge, regardless of the orientation of the ellipse. This distinction is crucial for accurately graphing and understanding the properties of ellipses.
Interestingly, the equations of ellipses share a resemblance with the equation of a circle. The standard equation of a circle is given by:
\[ x^2 + y^2 = r^2 \]
By dividing through by \( r^2 \), it can be rewritten as:
\[ \frac{x^2}{r^2} + \frac{y^2}{r^2} = 1 \]
This form highlights the symmetry of the circle, where the radius is uniform in all directions. In contrast, the ellipse equations reflect the varying distances \( a \) and \( b \), indicating the lack of uniform symmetry.
Understanding these concepts lays the groundwork for further exploration of ellipses, including their properties, applications, and the relationships they share with other conic sections.