Asymptotes: Videos & Practice Problems

Understanding rational functions involves identifying vertical and horizontal asymptotes, which are crucial for graphing. Vertical asymptotes occur where the denominator equals zero, while horizontal asymptotes depend on the degrees of the numerator and denominator. If the degree of the numerator is less than that of the denominator, the horizontal asymptote is at $y=0$. If they are equal, divide the leading coefficients. Additionally, common factors can create holes in the graph, represented by open circles. Understanding these concepts is essential for accurately graphing rational functions.

Introduction to Asymptotes

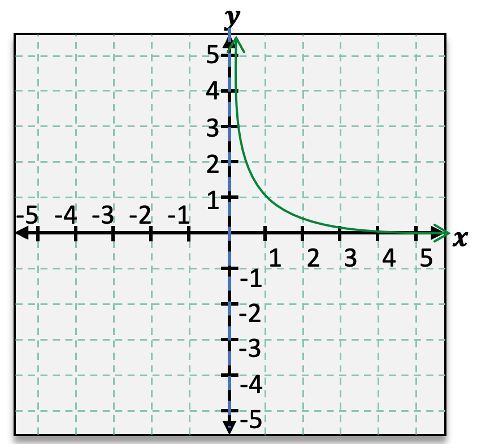
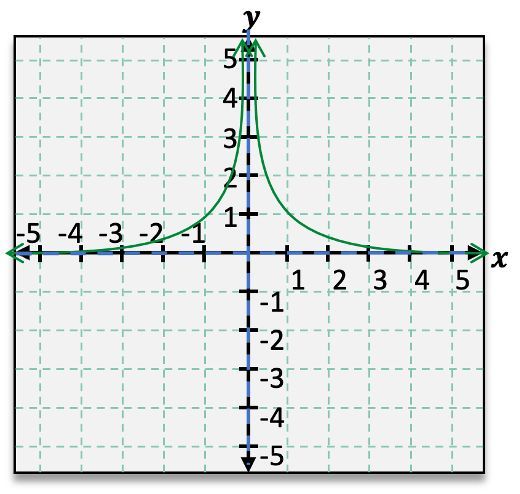
When analyzing rational functions, understanding asymptotes is crucial for accurately graphing these functions. Asymptotes are lines that the graph approaches but never touches, providing insight into the function's behavior at extreme values. For instance, consider the rational function \( f(x) = \frac{1}{x} \). This function exhibits both horizontal and vertical asymptotes.

To identify the horizontal asymptote, we observe the behavior of the function as \( x \) approaches infinity or negative infinity. In this case, as \( x \) approaches infinity, \( f(x) \) approaches 0, indicating a horizontal asymptote at \( y = 0 \). Similarly, as \( x \) approaches negative infinity, \( f(x) \) also approaches 0. This behavior can be expressed using limit notation: \( \lim_{x \to \infty} f(x) = 0 \) and \( \lim_{x \to -\infty} f(x) = 0 \).

Next, we examine the vertical asymptote, which occurs where the function is undefined. For \( f(x) = \frac{1}{x} \), the function is undefined at \( x = 0 \). As \( x \) approaches 0 from the right, \( f(x) \) approaches positive infinity, while from the left, it approaches negative infinity. This can be denoted as \( \lim_{x \to 0^+} f(x) = \infty \) and \( \lim_{x \to 0^-} f(x) = -\infty \). The vertical asymptote is represented by the dashed line \( x = 0 \).

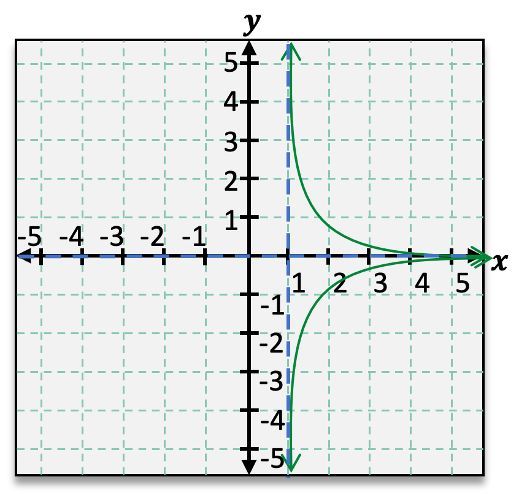
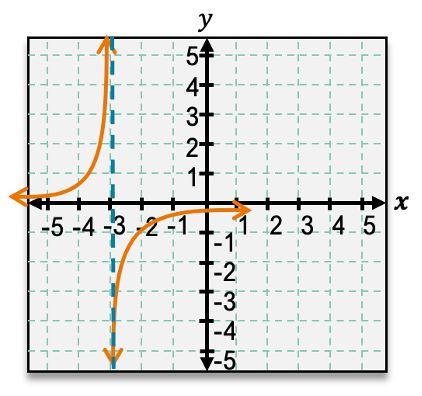
Rational functions can have various configurations of asymptotes. Some may have no asymptotes, while others can have one or multiple vertical and horizontal asymptotes. The presence and location of these asymptotes depend on the specific function being analyzed. Understanding these concepts is essential for graphing rational functions effectively and interpreting their behavior accurately.

Sketch the graph of the function $f\left(x\right)=\frac{1}{x^2}$. Identify the asymptotes on the graph.

• A. Vertical Asymptote: $x=0$, Horizontal Asymptote: None
• B. Vertical Asymptote: $x=0$, Horizontal Asymptote: $y=0$
• C. Vertical Asymptote: $x=0$, Horizontal Asymptote: $y=0$
• D. Vertical Asymptote: $x=1$ , Horizontal Asymptote: $y=0$

Answer: (C)

Determining Vertical Asymptotes

Understanding vertical asymptotes is crucial when analyzing rational functions. To determine the location of vertical asymptotes, we follow a straightforward process that mirrors finding the domain of the function. The key step is to set the denominator of the rational function equal to zero and solve for the variable.

Before proceeding, it is essential to express the function in its lowest terms. This involves factoring and canceling any common factors in the numerator and denominator. For example, consider the function:

\[f(x) = \frac{x + 2}{2(x - 3)}\]

First, we simplify the function by canceling the common factor of \(x + 2\), resulting in:

\[f(x) = \frac{1}{x - 3}\]

Next, we set the denominator equal to zero:

\[x - 3 = 0\]

Solving this gives us:

\[x = 3\]

This indicates that there is a vertical asymptote at \(x = 3\).

Let’s explore another example:

\[f(x) = \frac{2}{2x + 6}\]

Here, we factor the denominator to find the greatest common factor:

\[2x + 6 = 2(x + 3)\]

After canceling the common factor of 2, we have:

\[f(x) = \frac{1}{x + 3}\]

Setting the denominator to zero gives:

\[x + 3 = 0\]

Thus, we find:

\[x = -3\]

This means there is a vertical asymptote at \(x = -3\).

In a third example, consider:

\[f(x) = \frac{1}{x^2 - 9}\]

Since the numerator is already in its simplest form, we focus on the denominator. We set it equal to zero:

\[x^2 - 9 = 0\]

Solving this equation involves adding 9 to both sides:

\[x^2 = 9\]

Taking the square root of both sides yields:

\[x = \pm 3\]

Consequently, there are two vertical asymptotes: one at \(x = 3\) and another at \(x = -3\). It is important to note that having multiple vertical asymptotes is a common occurrence in rational functions.

With these examples, you should now feel confident in identifying vertical asymptotes in various rational functions. Practice with different functions to reinforce your understanding of this concept.

Based only on the vertical asymptotes, which of the following graphs could be the graph of the given function? $f\left(x\right)=\frac{x^2-4x}{x^2-x-12}$

• A.
• B.
• C.

Answer: (B)

Determining Removable Discontinuities (Holes)

When analyzing rational functions, it's essential to identify both vertical asymptotes and holes in the graph. Vertical asymptotes occur when the denominator of a function approaches zero, while holes, also known as removable discontinuities, arise from common factors in the numerator and denominator that can be canceled out.

To find vertical asymptotes, you typically factor the function and set the denominator equal to zero. For example, if you have a function where the denominator factors to include a term like \(x - 3\), setting this equal to zero reveals a vertical asymptote at \(x = 3\).

However, to locate holes in the graph, you should identify any common factors in both the numerator and denominator without canceling them out. Instead, set these common factors equal to zero. For instance, if a common factor is \(x + 2\), solving \(x + 2 = 0\) gives \(x = -2\), indicating a hole at this point on the graph, which is represented by an open circle.

Consider the function \(f(x) = \frac{x + 3}{x^2 + 4x + 3}\). Factoring the denominator yields \(f(x) = \frac{x + 3}{(x + 3)(x + 1)}\). Here, the common factor \(x + 3\) leads to a hole at \(x = -3\) when set to zero.

In another example, for the function \(f(x) = \frac{x^2 + 1}{x - 1}\), the numerator can be factored as \((x + 1)(x - 1)\). The common factor \(x - 1\) indicates a hole at \(x = 1\) when set to zero.

Understanding how to find holes in rational functions is crucial for accurately graphing these functions and interpreting their behavior. By recognizing both vertical asymptotes and holes, you can create a more complete picture of the function's graph.

Find all vertical asymptotes and holes of each function.
$f\left(x\right)=\frac{-5x}{\left(2x-3\right)^2}$

• A. Hole(s): $x=0$ , Vertical Asymptote(s): $x=\frac32$
• B. Hole(s): $x=\frac32$ , Vertical Asymptote(s): $x=\frac32$
• C. Hole(s): $x=0$ , Vertical Asymptote(s): $x=0$
• D. Hole(s): None , Vertical Asymptote(s): $x=\frac32$

Answer: (D)

Find all vertical asymptotes and holes of each function.
$f\left(x\right)=\frac{x^2-2x}{2x^3-x^2-6x}$

• A. Hole(s): None, Vertical Asymptote(s): $x=0,x=2,x=-\frac32$
• B. Hole(s): $x=0$, Vertical Asymptote(s): $x=-\frac32$
• C. Hole(s): $x=0$, $x=2$, Vertical Asymptote(s): $x=-\frac32$
• D. Hole(s): $x=0$, $x=2$, Vertical Asymptote(s): $x=\frac32$

Answer: (C)

Find all vertical asymptotes and holes of each function.
$f\left(x\right)=\frac{x^2+10x+25}{2x^2+8x-10}$

• A. Hole(s): None, Vertical Asymptote(s): $x=-5,$ $x=1$
• B. Hole(s): $x=-5$ , Vertical Asymptote(s): $x=1$
• C. Hole(s): $x=1$ , Vertical Asymptote(s): $x=-5$
• D. Hole(s): $x=-5$ , Vertical Asymptote(s): $x=-1$

Answer: (B)

Determining Horizontal Asymptotes

Understanding horizontal asymptotes is crucial for analyzing the behavior of rational functions, particularly how they influence the range. Unlike vertical asymptotes, which affect the domain, horizontal asymptotes are determined by the degrees of the numerator and denominator of a rational function.

To find a horizontal asymptote, you need to compare the degrees of the numerator and denominator. The degree of a polynomial is the highest power of the variable in that polynomial. Here are the key scenarios:

1. **Degree of the Numerator < Degree of the Denominator**: If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is at y = 0. For example, in the function f(x) = 1/x, the degree of the numerator is 0 and the degree of the denominator is 1, leading to a horizontal asymptote at y = 0.

2. **Degree of the Numerator = Degree of the Denominator**: If the degrees are equal, the horizontal asymptote can be found by dividing the leading coefficients of the numerator and denominator. For instance, in the function f(x) = (2x + 3)/x, both the numerator and denominator have a degree of 1. The leading coefficient of the numerator is 2, and the leading coefficient of the denominator is 1, resulting in a horizontal asymptote at y = 2/1 = 2.

3. **Degree of the Numerator > Degree of the Denominator**: If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote. Instead, the function may approach infinity or negative infinity as x approaches infinity.

For example, consider the function f(x) = 4x²/(-x³ - 5x + 9). The degree of the numerator is 2, and the degree of the denominator is 3. Since 2 is less than 3, the horizontal asymptote is at y = 0.

In another example, f(x) = 2x²/(3x² + x - 1), both the numerator and denominator have a degree of 2. The leading coefficient of the numerator is 2, and that of the denominator is 3, giving a horizontal asymptote at y = 2/3.

It’s also important to note that while horizontal asymptotes indicate the behavior of a function as x approaches infinity, the graph of the function may cross the horizontal asymptote. This phenomenon does not contradict the definition of asymptotes; it simply reflects the function's behavior in certain intervals.

By mastering these concepts, you can effectively analyze rational functions and their asymptotic behavior, enhancing your understanding of their graphical representations.

Find the horizontal asymptote of each function.
$f\left(x\right)=\frac{-5x}{\left(2x+3\right)^2}$

• A. Horizontal Asymptote at $y=0$
• B. Horizontal Asymptote at $y=-\frac54$
• C. Horizontal Asymptote at $y=-\frac52$

Answer: (A)

Find the horizontal asymptote of each function.
$f\left(x\right)=\frac{8x^2+1}{2x^2-x-6}$

• A. Horizontal Asymptote at $y=0$
• B. Horizontal Asymptote at $y=\frac14$
• C. Horizontal Asymptote at $y=4$

Answer: (C)

Find the horizontal asymptote of each function.
$f\left(x\right)=\frac{x^2+4x}{2x^3+8x^2}$

• A. Horizontal Asymptote at $y=0$
• B. Horizontal Asymptote at $y=\frac12$
• C. Horizontal Asymptote at $y=2$

Answer: (A)

Here’s what students ask on this topic:

What are vertical asymptotes and how do you find them?

Vertical asymptotes are lines that a graph approaches but never touches or crosses. They occur where the denominator of a rational function equals zero, causing the function to be undefined. To find vertical asymptotes, follow these steps:

1. Write the function in its lowest terms by canceling any common factors.
2. Set the denominator equal to zero.
3. Solve for $x$.

For example, for the function $\frac{1}{x^2-9}$, set $x^2-9=0$ and solve to get $x=\pm 3$. Thus, the vertical asymptotes are at $x=3$ and $x=-3$.

How do you determine horizontal asymptotes of a rational function?

Horizontal asymptotes depend on the degrees of the numerator and denominator of a rational function. Follow these rules:

1. If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is $y=0$.
2. If the degrees are equal, divide the leading coefficients of the numerator and denominator.
3. If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.

For example, for $\frac{2x^2+3}{3x^2+x-1}$, the degrees are equal, so the horizontal asymptote is $y=\frac{2}{3}$.

What is a hole in the graph of a rational function and how do you find it?

A hole in the graph of a rational function, also known as a removable discontinuity, occurs where a common factor in the numerator and denominator cancels out. To find a hole:

1. Factor the numerator and denominator.
2. Identify and cancel the common factor.
3. Set the common factor equal to zero and solve for $x$.

For example, for $\frac{x+3}{x^2+4x+3}$, factor to get $\frac{x+3}{x+3x+1}$. The common factor $x+3$ cancels, leaving a hole at $x=-3$.

Can a rational function cross its horizontal asymptote?

Yes, a rational function can cross its horizontal asymptote. While asymptotes are lines that the graph approaches, it is possible for the graph to intersect a horizontal asymptote and then approach it from the other side. This behavior does not contradict the definition of an asymptote, as the function still approaches the asymptote as $x$ approaches infinity or negative infinity. However, this crossing typically occurs in the middle of the graph, not at the extremes. Understanding this can help you accurately graph rational functions and interpret their behavior.

How do vertical asymptotes affect the domain of a rational function?

Vertical asymptotes affect the domain of a rational function by indicating values of $x$ where the function is undefined. These occur where the denominator equals zero. To find these values, set the denominator equal to zero and solve for $x$. The solutions are excluded from the domain. For example, for $\frac{1}{x-3}$, set $x-3=0$ to get $x=3$. Thus, $x=3$ is not in the domain.